Campo de un solenoide cilíndrico
De Laplace
(Nueva página: ==Enunciado== Un solenoide de radio <math>a</math>, altura <math>h</math> y <math>n</math> espiras por unidad de longitud, puede aproximarse por una distribución de corriente superfi...) |
(→Densidad superficial de corriente) |
||
| Línea 7: | Línea 7: | ||
==Densidad superficial de corriente== | ==Densidad superficial de corriente== | ||
| + | Dada una densidad de corriente superficial, la relación entre ésta y la intensidad de corriente total que atraviesa una línea trazada en la superficie es | ||
| + | |||
| + | <math>I_T=\int \mathbf{K}{\cdot}\mathbf{n}_1\,\mathrm{d}l</math> | ||
| + | |||
| + | donde <math>\mathbf{n}_1</math> es un vector unitario normal a la curva y tangente a la superficie. | ||
| + | |||
| + | Para establecer la correspondencia entre la corriente que circula por el solenoide y la densidad de corriente equivalente, imponemos que sea idéntica la corriente total que atraviesa una línea vertical trazada sobre el solenoide. Esta línea corta $N$ espiras, siendo | ||
| + | |||
| + | <center><math>N=nh\,</math></center> | ||
| + | |||
| + | por lo que la corriente total que atraviesa la línea es | ||
| + | |||
| + | <math>I_T=NI=nhI\,</math> | ||
| + | |||
| + | con <math>I</math> la intensidad que circula por cada espira. Si se supone una densidad de corriente superficial <math>\mathbf{K}=K\mathbf{u}_{\varphi}</math> resulta | ||
| + | |||
| + | <center><math>I_T=\int_0^h(K\mathbf{u}_{\varphi}){\cdot}\mathbf{u}_{\varphi}\,\mathrm{d}z=Kh</math></center> | ||
| + | |||
| + | Igualando ambas cantidades se tiene la relación | ||
| + | |||
| + | <center><math>K=nI\,</math></center> | ||
| + | |||
| + | o, equivalentemente <math>K=NI/h</math>. | ||
| + | |||
==Campo en un solenoide infinito== | ==Campo en un solenoide infinito== | ||
==Campo en un solenoide finito== | ==Campo en un solenoide finito== | ||
[[Categoría:Problemas de campo magnético de corrientes estacionarias]] | [[Categoría:Problemas de campo magnético de corrientes estacionarias]] | ||
Revisión de 12:47 12 abr 2009
Contenido |
1 Enunciado
Un solenoide de radio a, altura h y n espiras por unidad de longitud, puede aproximarse por una distribución de corriente superficial sobre un cilindro.
- Halle el valor
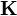equivalente a que por las espiras circule una corriente I.
- Empleando las leyes de la magnetostática, calcule el campo producido por el solenoide, si
.
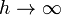- Mediante integración directa, halle el campo magnético en los puntos del eje del cilindro si h es finito. Estudie el límite
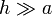
2 Densidad superficial de corriente
Dada una densidad de corriente superficial, la relación entre ésta y la intensidad de corriente total que atraviesa una línea trazada en la superficie es
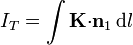
donde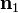 
es un vector unitario normal a la curva y tangente a la superficie.
Para establecer la correspondencia entre la corriente que circula por el solenoide y la densidad de corriente equivalente, imponemos que sea idéntica la corriente total que atraviesa una línea vertical trazada sobre el solenoide. Esta línea corta $N$ espiras, siendo
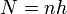
por lo que la corriente total que atraviesa la línea es
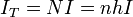
con I la intensidad que circula por cada espira. Si se supone una densidad de corriente superficial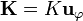 
resulta
Igualando ambas cantidades se tiene la relación
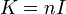
o, equivalentemente K = NI / h.
