Corrientes de magnetización
De Laplace
(Diferencias entre revisiones)
(→Imán cilíndrico) |
(→Imán cilíndrico) |
||
| Línea 24: | Línea 24: | ||
:* En las bases se anulan, por ser paralelos el vector normal y la imanación | :* En las bases se anulan, por ser paralelos el vector normal y la imanación | ||
| - | <center><math>\mathbf{K}_m=\mathbf{M}_0\times\mathbf{n}=(M_0\mathbf{u}_z)\times(\pm\mathbf{u}_z)=\ | + | <center><math>\mathbf{K}_m=\mathbf{M}_0\times\mathbf{n}=(M_0\mathbf{u}_z)\times(\pm\mathbf{u}_z)=\mathhbf{0}</math></center> |
:* En la cara lateral resulta una corriente acimutal | :* En la cara lateral resulta una corriente acimutal | ||
Revisión de 15:53 2 abr 2009
Contenido |
1 Definición
1.1 Transformación del potencial vector
1.2 Definición de las corrientes
1.2.1 Volumétricas
1.2.2 Superficiales
2 Interpretación física
3 Ejemplos
3.1 Imán cilíndrico
Artículo completo: Imán cilíndrico
Supongamos un cilindro de radio R y longitud L imanado axialmente con una magnetización uniforme 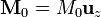 . Para este imán
. Para este imán
- Las corrientes volumétricas de magnetización son nulas:
- En el interior, por ser uniforme la imanación
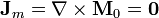
- En el exterior, por no haber magnetización
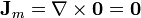
- Para las corrientes superficiales debemos distinguir entre las bases y la cara lateral
- En las bases se anulan, por ser paralelos el vector normal y la imanación
- En la cara lateral resulta una corriente acimutal
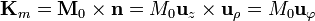
Por tanto, un imán cilíndrico es equivalente a un solenoide cilíndrico.





