Campo magnético debido a una magnetización
De Laplace
(→Demostración) |
(→Demostración) |
||
| Línea 23: | Línea 23: | ||
Hasta aquí no hay aproximación alguna. Dado que los elementos de volumen son microscópicos, podemos suponer que todos los dipolos de cada elemento se encuentran en la misma posición <math>\mathbf{r}'</math> | Hasta aquí no hay aproximación alguna. Dado que los elementos de volumen son microscópicos, podemos suponer que todos los dipolos de cada elemento se encuentran en la misma posición <math>\mathbf{r}'</math> | ||
| - | <center><math>\mathbf{A}\simeq\frac{\mu_0}{4\pi}\sum_{\Delta\tau}\left(\left(\sum_{\mathbf{m}_i\in\Delta\tau}\mathbf{m}_i\right)\times\frac{ | + | <center><math>\mathbf{A}\simeq\frac{\mu_0}{4\pi}\sum_{\Delta\tau}\left(\left(\sum_{\mathbf{m}_i\in\Delta\tau}\mathbf{m}_i\right)\times\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\right)</math></center> |
y, por la definición de [[magnetización]] | y, por la definición de [[magnetización]] | ||
| - | <center><math>\mathbf{A}\simeq\frac{\mu_0}{4\pi}\sum_{\Delta\tau}\left(\Delta\tau'\mathbf{M}(\mathbf{}')\times\frac{ | + | <center><math>\mathbf{A}\simeq\frac{\mu_0}{4\pi}\sum_{\Delta\tau}\left(\Delta\tau'\mathbf{M}(\mathbf{}')\times\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\right)</math></center> |
En el límite, este sumatorio se convierte en una integral | En el límite, este sumatorio se convierte en una integral | ||
| - | <center><math>\mathbf{A}=\frac{\mu_0}{4\pi}\int_\tau\mathbf{M}(\mathbf{}')\times\frac{ | + | <center><math>\mathbf{A}=\frac{\mu_0}{4\pi}\int_\tau\mathbf{M}(\mathbf{}')\times\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\mathrm{d}\tau'</math></center> |
==Campo magnético== | ==Campo magnético== | ||
Revisión de 08:35 2 abr 2009
Contenido |
1 Potencial vector
El potencial vector magnético debido a una magnetización es una extensión de la expresión correspondiente a un solo dipolo
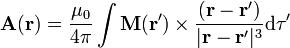
1.1 Demostración
La demostración es una consecuencia inmediata del principio de superposición. El potencial vector debido a un dipolo situado en el origen de coordenadas es
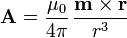
Si el dipolo no está en el origen, sino en el punto  , se efectúa una traslación
, se efectúa una traslación
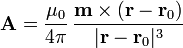
Si tenemos N dipolos, superponemos los potenciales respectivos
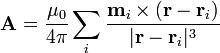
Para pasar a una distribución continua, organizamos el sumatorio, de forma que primero sumamos todos los dipolos que están dentro de un elemento y luego sumamos para todos los elementos
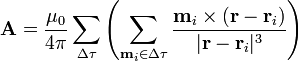
Hasta aquí no hay aproximación alguna. Dado que los elementos de volumen son microscópicos, podemos suponer que todos los dipolos de cada elemento se encuentran en la misma posición 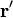
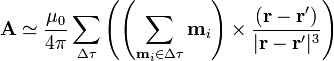
y, por la definición de magnetización
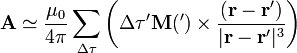
En el límite, este sumatorio se convierte en una integral
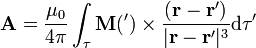
2 Campo magnético
Una vez que se tiene el potencial vector, puede hallarse el campo magnético

También puede calcularse a partir de la superposición del campo de dipolos magnéticos
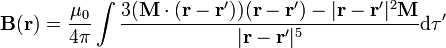
No obstante, la complejidad de estas integrales aconseja el uso de métodos alternativos de cálculo.





