Entrar Página Discusión Historial Go to the site toolbox

Imán cilíndrico

De Laplace

(Diferencias entre revisiones)
(→A partir de las cargas)
(→Comparación con los resultados anteriores)
Línea 195: Línea 195:
===Comparación con los resultados anteriores===
===Comparación con los resultados anteriores===
-
Ahora
+
Ahora que disponemos de la solución exacta, podemos comparar y juzgar las aproximaciones que hicimos antes. Según acabamos de ver, el campo exacto en el centro es
-
que disponemos de la solución exacta, podemos comparar y
+
-
juzgar las aproximaciones que hicimos antes. Según acabamos
+
-
de ver, el campo exacto en el centro es
+
-
\[
+
-
B=\frac{\mu_0 M L}{\sqrt{L^2+4R^2}}
+
-
\]
+
-
El valor numérico de este campo, para $L=1\,$mm es
+
-
\[
+
-
B=0.006275\,\mathrm{T}
+
-
\]
+
-
mientras que si $L=1\,$m
+
-
\[
+
-
B=0.125\,\mathrm{T}
+
-
\]
+
 +
<center><math>B=\frac{\mu_0 M L}{\sqrt{L^2+4R^2}}</math></center>
 +
 +
El valor numérico de este campo, para ''L'' = 1&thinsp;mm es
 +
 +
<center><math>B=0.006275\,\mathrm{T}</math></center>
 +
 +
mientras que si ''L'' = 1&thinsp;m
 +
 +
<center><math>B=0.125\,\mathrm{T}</math></center>
 +
 +
Para <math>H</math> tenemos, en general
 +
 +
<center><math>H=\frac{1}{\mu_0}B-M=-M_0\left(1-\frac{L}{\sqrt{L^2+4R^2}}\right)</math></center>
-
Para $H$ tenemos, en general
 
-
\[
 
-
H=\frac{1}{\mu_0}B-M=-M_0\left(1-\frac{L}{\sqrt{L^2+4R^2}}\right)
 
-
\]
 
resultando para el primer caso
resultando para el primer caso
-
\[H=
+
 
-
-95006.2 \frac{\mathrm{A}}{\mathrm{m}}
+
<center><math>H=-95006.2 \frac{\mathrm{A}}{\mathrm{m}}</math></center>
-
\]
+
 
y, para el segundo
y, para el segundo
-
\[
 
-
H=
 
-
-19.994 \frac{\mathrm{A}}{\mathrm{m}}
 
-
\]
 
 +
<center><math>H= -19.994 \frac{\mathrm{A}}{\mathrm{m}}</math></center>
 +
 +
Más interesante que el valor numérico puede ser la estimación de los términos despreciados. Si se tiene una expresión con un parámetro pequeño (en nuestro caso <math>L/R</math> o <math>R/L</math>, según el caso) y el desarrollo en serie de la solución exacta es es
 +
 +
<center><math>f_\mathrm{exacto}=f_0+\delta f_1+\delta^2 f_2+\cdots</math></center>
 +
 +
mientras que aproximadamente se han obtenido digamos dos términos
 +
 +
<center><math>f_\mathrm{aprox}= f_0+\delta f_1</math></center>
-
Más interesante que el valor numérico puede ser la
 
-
estimación de los términos despreciados. Si se tiene una
 
-
expresión con un parámetro pequeño (en nuestro caso $L/R$ o
 
-
$R/L$, según el caso) y el desarrollo en serie de la
 
-
solución exacta es es
 
-
\[
 
-
f_\mathrm{exacto}=f_0+\delta f_1+\delta^2 f_2+\cdots
 
-
\]
 
-
mientras que aproximadamente se han obtenido digamos dos
 
-
términos
 
-
\[
 
-
f_\mathrm{aprox}= f_0+\delta f_1
 
-
\]
 
entonces el error cometido es
entonces el error cometido es
-
\[
 
-
\epsilon_f=\frac{f_\mathrm{aprox}-f_\mathrm{exacto}}{f_\mathrm{exacto}}
 
-
\simeq \delta^2\frac{f_2}{f_0}
 
-
\]
 
-
de forma que podemos estimar el error cometido a partir de
 
-
los términos despreciados. La cantidad $f_2/f_0$ (o la
 
-
correspondiente a cada caso) suele ser una cantidad del
 
-
orden de la unidad, por lo que en realidad es $\delta$ el
 
-
que determina el error cometido.
 
-
\noindent \textbf{Caso $L\ll R$.} La expresión exacta puede
+
<center><math>\epsilon_f=\frac{f_\mathrm{aprox}-f_\mathrm{exacto}}{f_\mathrm{exacto}} \simeq \delta^2\frac{f_2}{f_0}</math></center>
-
desarrollarse en potencias de $L/R$, obteniéndose para $B$
+
 
-
\[
+
de forma que podemos estimar el error cometido a partir de los términos despreciados. La cantidad <math>f_2/f_0</math> (o la correspondiente a cada caso) suele ser una cantidad del orden de la unidad, por lo que en realidad es <math>\delta</math> el que determina el error cometido.
-
B=\frac{\mu_0 M_0 L}{2R}-\frac{\mu_0 M_0 L^3}{16R^3}+\cdots
+
 
-
\]
+
====Imán corto====
-
Antes obtuvimos sólo el primer término. Por tanto el error
+
La expresión exacta puede desarrollarse en potencias de <math>L/R</math>, obteniéndose para <math>B</math>
-
cometido es
+
 
-
\[
+
<center><math>B=\frac{\mu_0 M_0 L}{2R}-\frac{\mu_0 M_0 L^3}{16R^3}+\cdots</math></center>
-
\epsilon=\frac{B_\mathrm{aprox}-B_\mathrm{exacto}}{B_\mathrm{exacto}}
+
 
-
\simeq -\frac{L^2}{8R^2}=-0.00125
+
Antes obtuvimos sólo el primer término. Por tanto el error relativo cometido es
-
\]
+
 
-
mientras que para $H$ es aún menor ya que el desarrollo da
+
<center><math>\epsilon=\frac{B_\mathrm{aprox}-B_\mathrm{exacto}}{B_\mathrm{exacto}} \simeq -\frac{L^2}{8R^2}=-0.00125</math></center>
-
\[
+
 
-
H=-M_0+\frac{M_0 L}{2R}-\frac{M_0 L^3}{16R^3}+\cdots
+
mientras que para <math>H</math> es aún menor ya que el desarrollo da
-
\]
+
 
-
y nosotros obtuvimos los dos primeros términos. El error
+
<center><math>H=-M_0+\frac{M_0 L}{2R}-\frac{M_0 L^3}{16R^3}+\cdots</math></center>
-
para $H$ es, según esto,
+
 
-
\[
+
y nosotros obtuvimos los dos primeros términos. El error relativo para <math>H</math> es, según esto,
-
\epsilon_H=\frac{H_\mathrm{aprox}-H_\mathrm{exacto}}{H_\mathrm{exacto}}
+
 
-
\simeq \frac{L^3}{16R^2}=6.25\times 10^{-5}
+
<math>\epsilon_H=\frac{H_\mathrm{aprox}-H_\mathrm{exacto}}{H_\mathrm{exacto}} \simeq \frac{L^3}{16R^2}=6.25\times 10^{-5}</math>
-
\]
+
 
esto es, menos de una diezmilésima.
esto es, menos de una diezmilésima.
-
Para este mismo límite, empleando el modelo de cargas
+
Para este mismo límite, empleando el modelo de cargas magnéticas obtuvimos peores resultados, cuyo error se puede calcular de la misma manera.
-
magnéticas obtuvimos peores resultados, cuyo error se puede
+
-
calcular de la misma manera.
+
-
Igualmente se puede calcular el resultado para el caso del
+
Igualmente se puede calcular el resultado para el caso del disco y un punto situado encima de él.
-
disco y un punto situado encima de él.
+
 
 +
====Imán largo====
 +
Si el imán es muy largo, el desarrollo conveniente es en potencias de <math>R/L</math> y queda
 +
 
 +
<center><math>B=\mu_0 M_0 -\frac{2\mu_0 M_0 R^2}{L^2}+\frac{6\mu_0 M_0 R^4}{L^4}+\cdots</math></center>
 +
 
 +
De esta expresión nosotros, empleando el modelo de cargas puntuales, llegamos a los dos primeros términos. De aquí el error
 +
 
 +
<math>\epsilon_B\simeq \frac{6 R^4}{L^4}=6\times 10^{-8}</math>
-
\noindent\textbf{Caso $L\gg R$.} Si el imán es muy largo,
 
-
el desarrollo conveniente es en potencias de $R/L$ y queda
 
-
\[
 
-
B=\mu_0 M_0 -\frac{2\mu_0 M_0 R^2}{L^2}+\frac{6\mu_0 M_0
 
-
R^4}{L^4}+\cdots
 
-
\]
 
-
de esta expresión nosotros, empleando el modelo de cargas
 
-
puntuales, llegamos a los dos primeros términos. De aquí el
 
-
error
 
-
\[
 
-
\epsilon_B\simeq \frac{6 R^4}{L^4}=6\times 10^{-8}
 
-
\]
 
¡menos de una diezmillonésima!
¡menos de una diezmillonésima!
-
Para $H$ la aproximación es un poco peor
+
Para <math>H</math> la aproximación es un poco peor
-
\[
+
 
-
\epsilon_H\simeq \frac{3 R^2}{L^2}=3\times 10^{-4}
+
<center><math>\epsilon_H\simeq \frac{3 R^2}{L^2}=3\times 10^{-4}</math></center>
-
\]
+
 
-
De nuevo, en este límite, uno de los modelos (en este caso,
+
De nuevo, en este límite, uno de los modelos (en este caso, el de las corrientes superficiales) daba un resultado peor que el otro.
-
el de las corrientes superficiales) daba un resultado peor
+
 
-
que el otro.
+
Igualmente se calcula el error cometido a la hora de hallar el campo justo fuera del imán. La expresión exacta es
 +
 
 +
<center><math>B=\frac{\mu_0 M_0}{2}-\frac{\mu_0 M_0 R^2}{4L^2}+\frac{3\mu_0 M_0 R^4}{16 L^4}+\cdots</math></center>
 +
 
 +
y la expresión aproximada contenía sólo los dos primeros términos. El error vuelve a ser de diezmillonésimas, tanto para <math>B</math> como para <math>H</math>.
-
Igualmente se calcula el error cometido a la hora de hallar
+
Dado que normalmente hay otras fuentes de error mucho más importante, la principal de las cuales es que no se puede conseguir un imán con una magnetización uniforme, se ve que el cálculo aproximado puede interesar más que la complicada expresión integral. Por supuesto, es ''imprescindible'' disponer de una estimación del error cometido. Pero, según acabamos de ver, para esta estimación no es preciso conocer
-
el campo justo fuera del imán. La expresión exacta es
+
la solución exacta, sino saber de que orden es el primer término despreciado, y este orden viene dado por una potencia del parámetro  pequeño.
-
\[
+
-
B=\frac{\mu_0 M_0}{2}-\frac{\mu_0 M_0
+
-
R^2}{4L^2}+\frac{3\mu_0 M_0 R^4}{16 L^4}+\cdots
+
-
\]
+
-
y la expresión aproximada contenía sólo los dos primeros
+
-
términos. El error vuelve a ser de diezmillonésimas, tanto
+
-
para $B$ como para $H$.
+
-
Dado que normalmente hay otras fuentes de error mucho más
 
-
importante, la principal de las cuales es que no se puede
 
-
conseguir un imán con una magnetización uniforme, se ve que
 
-
el cálculo aproximado puede interesar más que la complicada
 
-
expresión integral. Por supuesto, es \emph{imprescindible}
 
-
disponer de una estimación del error cometido. Pero, según
 
-
acabamos de ver, para esta estimación no es preciso conocer
 
-
la solución exacta, sino saber de que orden es el primer
 
-
término despreciado, y este orden viene dado por una
 
-
potencia del parámetro pequeño.
 
[[Categoría:Problemas de materiales magnéticos]]
[[Categoría:Problemas de materiales magnéticos]]

Revisión de 18:39 31 mar 2009

Contenido

1 Enunciado

Se construye un imán cilíndrico de radio R = 1cm y longitud L, con una magnetización uniforme y paralela a su eje M0 = 105A / m.

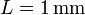  1. Determine aproximadamente los campos \mathbf{H} y \mathbf{B} cuando L=1\,\mathrm{mm}, en el centro del imán y en un punto ligeramente por encima de su base superior.
    1. A partir de las corrientes de magnetización.
    2. A partir de las cargas magnéticas.
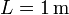  2. Estime \mathbf{H} y \mathbf{B} cuando L=1\,\mathrm{m} en los mismos puntos y con los mismos métodos
  3. Determine exactamente \mathbf{H} y \mathbf{B} en todos los puntos del eje del imán, tanto dentro como fuera de él. Compare con los resultados anteriores

2 Imán corto

Cuando el imán se reduce a un disco, porque 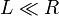L\ll R, como ocurre en este caso (R = 1 cm, L = 1 mm), podemos calcular el campo de dos formas: empleando las corrientes de magnetización, o empleando las cargas magnéticas

2.1 Empleando las corrientes

Por ser la imanación 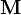\mathbf{M} uniforme, no hay corrientes de volumen, pero sí superficiales. Puesto que la magnetización es perpendicular a las bases del disco, las únicas corrientes de imanación están en la cara lateral y valen

\mathbf{K}_m=\mathbf{M}\times\mathbf{n}=M_0\mathbf{u}_{z}\times\mathbf{u}_{\rho}=M_0\mathbf{u}_{\varphi}

Así pues, el disco imanado es aproximadamente equivalente a una espira de corriente por la que circula una intensidad

I=M_0 L\,

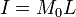
2.1.1 En el centro del imán

A partir de esta equivalencia, es inmediato conocer el campo \mathbf{B} en el centro del imán, pues el campo de una espira circular es un problema clásico con solución

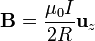
\mathbf{B}=\frac{\mu_0 I}{2R}\mathbf{u}_{z}

y en nuestro caso resulta un campo

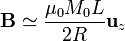
\mathbf{B}\simeq \frac{\mu_0 M_0L}{2R}\mathbf{u}_{z}

Una vez conocido el valor de \mathbf{B}, el cálculo de \mathbf{H} es inmediato

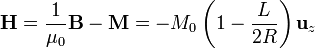
\mathbf{H}=\frac{1}{\mu_0}\mathbf{B}-\mathbf{M}=-M_0\left(1-\frac{L}{2R}\right)\mathbf{u}_{z}

Nótese que, de los dos términos del paréntesis, el segundo representa una corrección al primero, pues 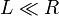L\ll R.

Los valores numéricos de estos dos campos en esta aproximación son (en el Sistema Internacional)

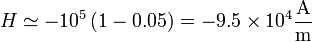
B \simeq 5\times 10^{3}\mu_0\simeq 6.28 \times 10^{-3}\,\mathrm{T}=6.28\,\mathrm{mT}        H\simeq -10^5\left(1-0.05\right)=-9.5\times 10^{4}\frac{\mathrm{A}}{\mathrm{m}}

2.1.2 Justo encima del imán

Para un punto ligeramente por encima del disco, el campo \mathbf{B} es el mismo pues la espira equivalente se puede considerar prácticamente como plana, pero el campo \mathbf{H} cambia pues en el exterior del imán la magnetización es nula (el vacío no se magnetiza). Esto da

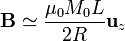
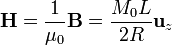
\mathbf{B}\simeq \frac{\mu_0 M_0 L}{2R}\mathbf{u}_{z}        \mathbf{H}=\frac{1}{\mu_0}\mathbf{B}=\frac{M_0 L}{2R}\mathbf{u}_{z}

2.2 Empleando las cargas

Este mismo sistema puede modelarse considerando densidades de carga magnética equivalentes. De nuevo, por ser la magnetización uniforme, no hay densidad volumétrica, pero sí superficial, dada por la expresión

\sigma_m=\mathbf{M}{\cdot}\mathbf{n}

En este caso, 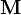\mathbf{M} es tangente a la cara lateral y sobre la misma no hay densidades de carga, pero sí sobre las bases. Sobre la cara superior será

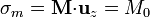
\sigma_m=\mathbf{M}{\cdot}\mathbf{u}_{z}=M_0

y, sobre la inferior

\sigma_m=\mathbf{M}{\cdot}(-\mathbf{u}_{z})=-M_0

esto es, el imán es equivalente a dos discos de carga de signos opuestos y muy próximos entre sí. Esto es el análogo magnético de lo que en electrostática es un condensador.

Sabemos que el campo eléctrico en un condensador de placas planas y paralelas, despreciando los efectos de borde, con densidad de carga σs en la cara positiva, es

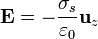
\mathbf{E}=-\frac{\sigma_s}{\varepsilon_0}\mathbf{u}_{z}

En nuestro caso, las ecuaciones para \mathbf{H} son las mismas que para \mathbf{E}, salvo que no aparece \varepsilon_0. Esto nos da para el campo \mathbf{H}

\mathbf{H}=-\sigma_m\mathbf{u}_{z}=-M_0\mathbf{u}_{z}

y, a partir de \mathbf{H}, se obtiene \mathbf{B}

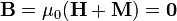
\mathbf{B}=\mu_0(\mathbf{H}+\mathbf{M})=\mathbf{0}

El valor numérico es inmediato

H\simeq -10^{5}\frac{\mathrm{A}}{\mathrm{m}}        B\simeq 0

Vemos que, en esta aproximación resulta un campo magnético nulo en el interior, mientras que antes resultaba un valor distinto de cero. Si comparamos las dos expresiones vemos que en este caso se ha despreciado la primera corrección, proporcional a L / R que allí sí aparecía.

En cuanto a un punto en el exterior, sabemos que fuera de un condensador el campo es nulo (aproximadamente), por lo que

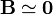
\mathbf{H}\simeq \mathbf{0}        \mathbf{B}\simeq \mathbf{0}

3 Imán largo

Cuando el imán es muy largo, podemos, de nuevo, obtener soluciones aproximadas por los dos modelos

3.1 Empleando las corrientes

Como antes, 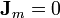\mathbf{J}_m=0 y la corriente superficial es

\mathbf{K}_m=\mathbf{M}\times\mathbf{n}=M_0\mathbf{u}_{\varphi}

pero ahora el imán no se puede sustituir por una espira, sino por un solenoide. Si el imán es muy largo (esto es, si L\gg R), podemos emplear el campo de un solenoide de longitud infinita, que es

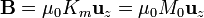
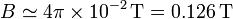
\mathbf{B}= \mu_0 K_m \mathbf{u}_{z}=\mu_0 M_0\mathbf{u}_{z}    B\simeq 4\pi \times 10^{-2}\,\mathrm{T}=0.126\,\mathrm{T}

y de aquí resulta para \mathbf{H}

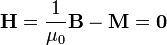
\mathbf{H}=\frac{1}{\mu_0}\mathbf{B}-\mathbf{M}=\mathbf{0}

Esto en lo que se refiere a un punto en el centro del imán. Para un punto justo por encima de la barra tenemos un problema en esta aproximación, y es que en un solenoide infinito no existe tal punto. Por tanto, carecemos de las expresiones para \mathbf{B} y \mathbf{H} en este punto.

Podríamos resolver el problema de un solenoide semiinfinito, pero la solución es casi tan compleja como la del solenoide de longitud finita, que veremos cuando analicemos la solución exacta, así que no merece la pena tal cálculo.

3.2 Empleando las cargas

Como antes, se verifica que

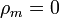
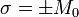
\rho_m=0\,        \sigma=\pm M_0

(con el signo dependiente de si estamos en la cara superior o en la inferior).

En este caso el sistema no es equivalente a un condensador, pues la separación entre las “placas” es mucho mayor que el tamaño de las mismas. Sin embargo, si estamos interesados en el campo en el centro del imán, podemos “ver” los discos de carga como dos cargas puntuales de valor

q_m=\pm M_0 S=\pm \pi M_0 R^2

El campo creado por estas dos cargas en un punto situado a L / 2 de ambas es análogo a un campo eléctrico (sin el factor \varepsilon_0)

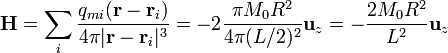
\mathbf{H}=\sum_i \frac{q_{mi}(\mathbf{r}-\mathbf{r}_i)}{4\pi|\mathbf{r}-\mathbf{r}_i|^3}= -2\frac{\pi M_0 R^2}{4\pi (L/2)^2}\mathbf{u}_{z}=-\frac{2M_0R^2}{L^2}\mathbf{u}_{z}

y, a partir de \mathbf{H}, llegamos a \mathbf{B}

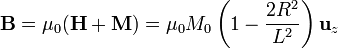
\mathbf{B}=\mu_0(\mathbf{H}+\mathbf{M})=\mu_0M_0\left(1-\frac{2R^2}{L^2}\right)\mathbf{u}_{z}

Los valores numéricos para estos campos son

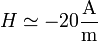
H\simeq -20\frac{\mathrm{A}}{\mathrm{m}}        B\simeq 10^5\mu_0\left(1-0.0002\right)\simeq 0.126\,\mathrm{T}

Vemos que, inversamente a lo que ocurrió en el límite anterior, en este caso es más exacto el modelo de cargas magnéticas que el de corrientes, pues obtenemos un término de orden (R / L)2 que antes no apareció. En cualquier caso, la diferencia entre las dos aproximaciones es muy pequeña, pues el nuevo termino incluido vale el 0.02% del anterior.

Para un punto próximo a la superficie no nos vale el campo de una carga puntual en lo que se refiere al disco próximo, sí al que está alejado. En su lugar empleamos el campo de un disco de carga uniforme, que se calcula en electrostática. Para un punto infinitamente cercano a la superficie es

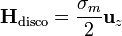
\mathbf{H}_\mathrm{disco}=\frac{\sigma_m}{2}\mathbf{u}_{z}

Sumando este campo con el de la carga puntual equivalente a la cara lejana (situada a una distancia L) queda

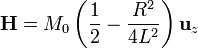
\mathbf{H}=M_0\left(\frac{1}{2}-\frac{R^2}{4L^2}\right)\mathbf{u}_{z}

En el aire \mathbf{B} y \mathbf{H} son simplemente proporcionales, así que

\mathbf{B}=\mu_0\mathbf{H}=\mu_0M_0\left(\frac{1}{2}-\frac{R^2}{4L^2}\right)\mathbf{u}_{z}

En cuanto al valor numérico de estos campos, se tiene

H=10^5\left(0.5-0.000025\right)\simeq 4.999975\times 10^4\frac{\mathrm{A}}{\mathrm{m}}        B=62.83\,\mathrm{mT}

4 Imán de longitud arbitraria

4.1 A partir de las corrientes

Las corrientes equivalentes son las de un solenoide de longitud finita. El campo magnético para los puntos del eje (suponiendo el cilindro centrado en el eje y extendiéndose desde − L / 2 a L / 2) corresponde a la expresión

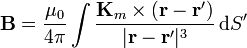
\mathbf{B}=\frac{\mu_0}{4\pi} \int \frac{\mathbf{K}_m\times(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\,\mathrm{d}S'

con 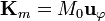\mathbf{K}_m=M_0\mathbf{u}_{\varphi} en la superficie lateral y nula en el resto.

Este problema se resuelve, para el caso de una corriente libre, en el problema del solenoide finito. La solución es

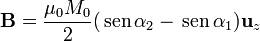
\mathbf{B}=\frac{\mu_0M_0}{2}(\,\mathrm{sen}\,\alpha_2-\,\mathrm{sen}\,\alpha_1)\mathbf{u}_{z}

donde α1 y α2 son los ángulos con que se ven los extremos del imán desde un punto del eje.

En el punto central del imán α2 = − α1 con

\,\mathrm{sen}\,\alpha_2=\frac{L/2}{\sqrt{(L/2)^2+R^2}}=\frac{L}{\sqrt{L^2+4R^2}}

y

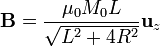
\mathbf{B}=\frac{\mu_0M_0L}{\sqrt{L^2+4R^2}}\mathbf{u}_{z}

En el extremo superior, en cambio,

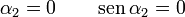
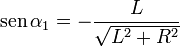
\alpha_2=0\qquad\,\mathrm{sen}\,\alpha_2=0        \,\mathrm{sen}\,\alpha_1=-\frac{L}{\sqrt{L^2+R^2}}

y el campo es

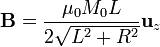
\mathbf{B}=\frac{\mu_0M_0 L}{2\sqrt{L^2+R^2}}\mathbf{u}_{z}

A partir de B obtenemos el campo H. Para los puntos del interior del imán ( − L / 2 < z < L / 2) resulta

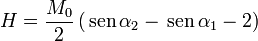
H=\frac{M_0}{2}\left(\,\mathrm{sen}\,\alpha_2-\,\mathrm{sen}\,\alpha_1-2\right)

mientras que en el exterior es, simplemente

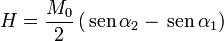
H=\frac{M_0}{2}\left(\,\mathrm{sen}\,\alpha_2-\,\mathrm{sen}\,\alpha_1\right)

La discontinuidad en este campo corresponde a la densidad de carga magnética equivalente a la magnetización.

4.2 A partir de las cargas

También podemos calcular el campo creado por dos discos de carga uniforme en todos los puntos de su eje. La solución será la superposición del campo de cada disco, cuyo valor se calcula en |un problema de electrostática.

El campo de un solo disco situado en z = 0 es

H=\frac{\sigma_m}{2}\left(\pm 1 -\frac{z}{\sqrt{R^2+z^2}}\right)

con el signo dependiente de si se está por encima o por debajo del disco.

Combinando este resultado para dos discos se llega a las mismas expresiones que en el apartado anterior.

4.3 Comparación con los resultados anteriores

Ahora que disponemos de la solución exacta, podemos comparar y juzgar las aproximaciones que hicimos antes. Según acabamos de ver, el campo exacto en el centro es

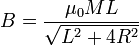
B=\frac{\mu_0 M L}{\sqrt{L^2+4R^2}}

El valor numérico de este campo, para L = 1 mm es

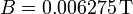
B=0.006275\,\mathrm{T}

mientras que si L = 1 m

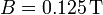
B=0.125\,\mathrm{T}

Para H tenemos, en general

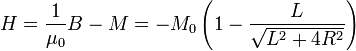
H=\frac{1}{\mu_0}B-M=-M_0\left(1-\frac{L}{\sqrt{L^2+4R^2}}\right)

resultando para el primer caso

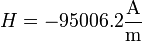
H=-95006.2 \frac{\mathrm{A}}{\mathrm{m}}

y, para el segundo

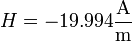
H= -19.994 \frac{\mathrm{A}}{\mathrm{m}}

Más interesante que el valor numérico puede ser la estimación de los términos despreciados. Si se tiene una expresión con un parámetro pequeño (en nuestro caso L / R o R / L, según el caso) y el desarrollo en serie de la solución exacta es es

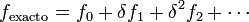
f_\mathrm{exacto}=f_0+\delta f_1+\delta^2 f_2+\cdots

mientras que aproximadamente se han obtenido digamos dos términos

faprox = f0 + δf1

entonces el error cometido es

\epsilon_f=\frac{f_\mathrm{aprox}-f_\mathrm{exacto}}{f_\mathrm{exacto}} \simeq \delta^2\frac{f_2}{f_0}

de forma que podemos estimar el error cometido a partir de los términos despreciados. La cantidad f2 / f0 (o la correspondiente a cada caso) suele ser una cantidad del orden de la unidad, por lo que en realidad es δ el que determina el error cometido.

4.3.1 Imán corto

La expresión exacta puede desarrollarse en potencias de L / R, obteniéndose para B

B=\frac{\mu_0 M_0 L}{2R}-\frac{\mu_0 M_0 L^3}{16R^3}+\cdots

Antes obtuvimos sólo el primer término. Por tanto el error relativo cometido es

\epsilon=\frac{B_\mathrm{aprox}-B_\mathrm{exacto}}{B_\mathrm{exacto}} \simeq -\frac{L^2}{8R^2}=-0.00125

mientras que para H es aún menor ya que el desarrollo da

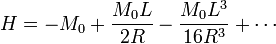
H=-M_0+\frac{M_0 L}{2R}-\frac{M_0 L^3}{16R^3}+\cdots

y nosotros obtuvimos los dos primeros términos. El error relativo para H es, según esto,

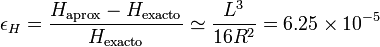
\epsilon_H=\frac{H_\mathrm{aprox}-H_\mathrm{exacto}}{H_\mathrm{exacto}} \simeq \frac{L^3}{16R^2}=6.25\times 10^{-5}

esto es, menos de una diezmilésima.

Para este mismo límite, empleando el modelo de cargas magnéticas obtuvimos peores resultados, cuyo error se puede calcular de la misma manera.

Igualmente se puede calcular el resultado para el caso del disco y un punto situado encima de él.

4.3.2 Imán largo

Si el imán es muy largo, el desarrollo conveniente es en potencias de R / L y queda

B=\mu_0 M_0 -\frac{2\mu_0 M_0 R^2}{L^2}+\frac{6\mu_0 M_0 R^4}{L^4}+\cdots

De esta expresión nosotros, empleando el modelo de cargas puntuales, llegamos a los dos primeros términos. De aquí el error

\epsilon_B\simeq \frac{6 R^4}{L^4}=6\times 10^{-8}

¡menos de una diezmillonésima!

Para H la aproximación es un poco peor

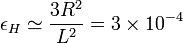
\epsilon_H\simeq \frac{3 R^2}{L^2}=3\times 10^{-4}

De nuevo, en este límite, uno de los modelos (en este caso, el de las corrientes superficiales) daba un resultado peor que el otro.

Igualmente se calcula el error cometido a la hora de hallar el campo justo fuera del imán. La expresión exacta es

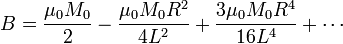
B=\frac{\mu_0 M_0}{2}-\frac{\mu_0 M_0 R^2}{4L^2}+\frac{3\mu_0 M_0 R^4}{16 L^4}+\cdots

y la expresión aproximada contenía sólo los dos primeros términos. El error vuelve a ser de diezmillonésimas, tanto para B como para H.

Dado que normalmente hay otras fuentes de error mucho más importante, la principal de las cuales es que no se puede conseguir un imán con una magnetización uniforme, se ve que el cálculo aproximado puede interesar más que la complicada expresión integral. Por supuesto, es imprescindible disponer de una estimación del error cometido. Pero, según acabamos de ver, para esta estimación no es preciso conocer la solución exacta, sino saber de que orden es el primer término despreciado, y este orden viene dado por una potencia del parámetro pequeño.

Obtenido de "http://tesla.us.es/wiki/index.php/Im%C3%A1n_cil%C3%ADndrico"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace