Integrales de superficie. Ejemplos
De Laplace
(→Cálculo de la integral) |
(→Primera integral) |
||
| Línea 25: | Línea 25: | ||
En el primer caso, se trata de hallar | En el primer caso, se trata de hallar | ||
| + | <center> | ||
| + | <math>\oint \mathbf{A}\cdot\mathrm{d}\mathbf{S}</math></center> | ||
| + | |||
| + | donde | ||
| + | |||
| + | <center><math>\mathbf{A} =\mathrm{cotg}\,\theta\mathbf{u}_{r}-\mathbf{u}_{\theta}</math></center> | ||
| + | |||
| + | y la superficie de integración es una esfera de radio <math>R</math> con centro el origen de coordenadas. | ||
Revisión de 20:31 23 nov 2007
Contenido |
1 Enunciado
Imaginemos que se nos pide calcular las dos integrales siguientes
donde
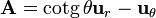
y la superficie de integración es una esfera de radio R con centro el origen de coordenadas.
Si no estamos atentos, podemos preguntarnos, ¿no son acaso la misma integral? ¿Qué diferencia hay entre ellas?
Con un poco de atención podemos ver que
- En la primera integral
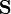aparece en negrita, mientras que en la segunda aparece en cursiva, S, lo cual quiere decir que en el primer caso se trata de un vector mientras que en el segundo se trata de un escalar.
- Para reforzar lo anterior, podemos ver que en la integral de la izquierda hay un puntito, que indica que se trata de un producto escalar, el cual no sería aplicable si se tratara de escalares
- Por tanto, en la primera integral el resultado es un número, mientras que en la segunda se trata de un vector.
Veamos cada integral por separado:
2 Primera integral
En el primer caso, se trata de hallar
donde
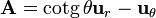
y la superficie de integración es una esfera de radio R con centro el origen de coordenadas.
2.1 Elección de coordenadas
Puesto que la superficie de integración es una esfera, es natural emplear coordenadas esféricas. En éstas, la superficie de integración es
![r = R\qquad \theta\in [0,\pi]\qquad\varphi \in [0,2\pi)](/wiki/images/math/a/b/2/ab2b6d62bda4037ac09352115cd60418.png)
y el diferencial de superficie correspondiente
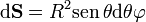
La función vectorial a integrar ya está en coordenadas esféricas, así que no hay que tocarla.
El producto escalar vale
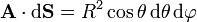
2.2 Cálculo de la integral
Sustituyendo lo anterior
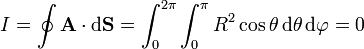
ya que la integral del coseno entre 0 y π es nula.
