Potencial vector magnético
De Laplace
(→Solenoide infinito) |
(→Solenoide infinito) |
||
| Línea 42: | Línea 42: | ||
La primera de las dos ecuaciones es una condición extra que siempre podemos imponer para determinar un potencial vector. La segunda ecuación nos dice que las fuentes vectoriales de <math>\mathbf{A}</math> son uniformes y en la dirección Z dentro de un cilindro de radio <math>a</math> y nulas en el exterior. Estas ecuaciones son completamente ''análogas'' a las que verifica el campo magnético respecto de la densidad de corriente en el caso de un [[Campo_magnético_de_un_cable_cilíndrico|cable grueso]]. Por ello, la expresión para el potencial vector es la ''análoga'' a la del campo magnético en ese sistema; | La primera de las dos ecuaciones es una condición extra que siempre podemos imponer para determinar un potencial vector. La segunda ecuación nos dice que las fuentes vectoriales de <math>\mathbf{A}</math> son uniformes y en la dirección Z dentro de un cilindro de radio <math>a</math> y nulas en el exterior. Estas ecuaciones son completamente ''análogas'' a las que verifica el campo magnético respecto de la densidad de corriente en el caso de un [[Campo_magnético_de_un_cable_cilíndrico|cable grueso]]. Por ello, la expresión para el potencial vector es la ''análoga'' a la del campo magnético en ese sistema; | ||
| - | <center><math>\mathbf{A}=\begin{cases}\displaystyle\frac{\mu_0nI\rho}{2}\mathbf{u}_\varphi & (\rho<a) \\ \displaystyle\frac{\mu_0nIa^2}{2\rho}\mathbf{u}_\varphi & (rho>a) \end{cases}</math></center> | + | <center><math>\mathbf{A}=\begin{cases}\displaystyle\frac{\mu_0nI\rho}{2}\mathbf{u}_\varphi & (\rho<a) \\ \displaystyle\frac{\mu_0nIa^2}{2\rho}\mathbf{u}_\varphi & (\rho>a) \end{cases}</math></center> |
===Dipolo magnético=== | ===Dipolo magnético=== | ||
Revisión de 18:13 23 mar 2009
Contenido |
1 Definición
De que el campo magnético sea solenoidal se deduce que puede escribirse como el rotacional de otro campo vectorial, denominado potencial vector magnético
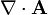
2 Expresión integral
Al demostrar la ley de Gauss para el campo magnético ya se da una expresión para este potencial vector
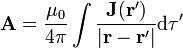
sin embargo, esta expresión, aparte de que sólo vale para corrientes estacionarias, no es la única posible.
3 Falta de unicidad
Dado un campo magnético, existen infinitos potenciales vectores posibles, los cuales se diferencian en el gradiente de una función escalar arbitraria
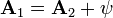
siendo la demostración inmediata, sin más que tomar el rotacional de ambos miembros. La libertad de elección de ψ hace que podamos tener potenciales vectores muy diferentes para el mismo campo.
4 Aplicaciones
La utilidad del potencial vector es limitada, por su naturaleza vectorial, que hace que no reduzca sustancialmente el problema del cálculo de 
.
Sirve como herramienta en los casos en que tenemos corrientes fluyendo siempre según la misma componente. Por ejemplo, si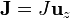 
podemos suponer 
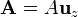. Si 
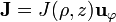podemos suponer 
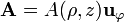. En estos casos el cálculo del potencial vector se reduce a determinar una sola componente, de forma similar a como se hace con el potencial escalar del campo electrostático.
La otra utilidad del potencial vector es su uso en deducciones teóricas acerca del campo magnético y para el electromagnético, Uno de estos casos es en el desarrollo multipolar magnético.
El potencial vector es útil a la hora de calcular flujos magnéticos, ya que
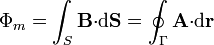
siendo S una superficie apoyada en Γ y orientada según la regla de la mano derecha.
5 Ejemplos
5.1 Solenoide infinito
Para un solenoide cilíndrico de radio a y longitud finita, el campo magnético, obtenido empleando las leyes de la magnetostática, es igual a
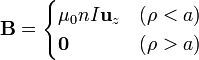
Un potencial vector del que deriva este campo cumple las ecuaciones
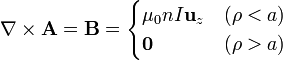
La primera de las dos ecuaciones es una condición extra que siempre podemos imponer para determinar un potencial vector. La segunda ecuación nos dice que las fuentes vectoriales de 
son uniformes y en la dirección Z dentro de un cilindro de radio a y nulas en el exterior. Estas ecuaciones son completamente análogas a las que verifica el campo magnético respecto de la densidad de corriente en el caso de un cable grueso. Por ello, la expresión para el potencial vector es la análoga a la del campo magnético en ese sistema;
5.2 Dipolo magnético
Para un dipolo magnético puntual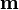 
, situado en el origen de coordenadas, el potencial vector es igual a
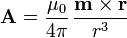
Esta expresión es análoga al potencial eléctrico de un dipolo eléctrico 
cambiando el producto escalar por el vectorial.
