Primera Convocatoria Ordinaria 2020/21 (MR G.I.C.)
De Laplace
(Diferencias entre revisiones)
(Página creada con '== Disco articulado en barra con extremo moviéndose en un raíl vertical == [[Archivo:M…') |
(→Disco articulado en barra con extremo moviéndose en un raíl vertical) |
||
| Línea 7: | Línea 7: | ||
en la figura. Una fuerza <math>\vec{F}=F_0\,\vec{\jmath}_1</math> actúa sobre el extremo <math>B</math> de la barra. | en la figura. Una fuerza <math>\vec{F}=F_0\,\vec{\jmath}_1</math> actúa sobre el extremo <math>B</math> de la barra. | ||
#Localiza gráficamente los C.I.R. de los tres movimientos relativos del sistema y escribe sus vectores de posición respecto a <math>O</math>. | #Localiza gráficamente los C.I.R. de los tres movimientos relativos del sistema y escribe sus vectores de posición respecto a <math>O</math>. | ||
| - | #Demuestra que existen dos ligaduras de la forma <math>\dot{s} + b\dot{\phi}\,\mathrm{sen}\,\phi=0, \quad c\,\dot{\theta}+d\dot{\phi}\,\mathrm{sen}\,{\phi}=0.</math> | + | #Demuestra que existen dos ligaduras de la forma <math>\dot{s} + b\dot{\phi}\,\mathrm{sen}\,\phi=0, \quad c\,\dot{\theta}+d\dot{\phi}\,\mathrm{sen}\,{\phi}=0.</math>. Encuentra los valores de los coeficientes <math>a, b, c, d</math>. |
| - | + | ||
#Escribe las reducciones cinemáticas de los movimientos absolutos de los dos sólidos en sus centros de masas respectivos. Deben quedar en función de <math>\phi</math> y <math>\dot{\phi}</math>. | #Escribe las reducciones cinemáticas de los movimientos absolutos de los dos sólidos en sus centros de masas respectivos. Deben quedar en función de <math>\phi</math> y <math>\dot{\phi}</math>. | ||
#Calcula la energía cinética total del sistema. | #Calcula la energía cinética total del sistema. | ||
#Dibuja los diagramas de fuerzas de los dos sólidos. | #Dibuja los diagramas de fuerzas de los dos sólidos. | ||
#Aplicando el T.C.M. y el T.M.C. encuentra las ecuaciones que describen el movimiento y las reacciones vinculares. No es necesario hacer las derivadas temporales al aplicar los teoremas. | #Aplicando el T.C.M. y el T.M.C. encuentra las ecuaciones que describen el movimiento y las reacciones vinculares. No es necesario hacer las derivadas temporales al aplicar los teoremas. | ||
Revisión de 18:07 17 feb 2021
Disco articulado en barra con extremo moviéndose en un raíl vertical
Un aro de masa m y radio R (sólido "2") rueda sin deslizar sobre una superficie rugosa
(eje fijo OX1). En el centro del aro se articula una varilla delgada de masa m y longitud
2R (sólido "0"). El otro extremo de la varilla se articula en un pasador que debe moverse en
un raíl fijo vertical. La distancia entre el eje OY1 y el raíl es 4R. La gravedad actúa como se indica
en la figura. Una fuerza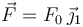 
actúa sobre el extremo B de la barra.
- Localiza gráficamente los C.I.R. de los tres movimientos relativos del sistema y escribe sus vectores de posición respecto a O.
- Demuestra que existen dos ligaduras de la forma
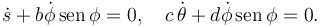. Encuentra los valores de los coeficientes a,b,c,d.
- Escribe las reducciones cinemáticas de los movimientos absolutos de los dos sólidos en sus centros de masas respectivos. Deben quedar en función de φ y
.
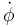- Calcula la energía cinética total del sistema.
- Dibuja los diagramas de fuerzas de los dos sólidos.
- Aplicando el T.C.M. y el T.M.C. encuentra las ecuaciones que describen el movimiento y las reacciones vinculares. No es necesario hacer las derivadas temporales al aplicar los teoremas.
