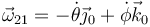Barra que desliza en eje rotatorio (CMR)
De Laplace
| Línea 55: | Línea 55: | ||
Esta corresponde a un movimiento de rotación alrededor de <math>{OZ}_1</math> | Esta corresponde a un movimiento de rotación alrededor de <math>{OZ}_1</math> | ||
| - | <center><math>\vec{v}^A_{01}=\vec{\omega}_{01}\times\overrightarrow{OA}=(\dot{\phi}\vec{k}_0)\times(b\,\mathrm{sen}(\theta)\vec{\imath}_0)=b\dot{\phi}\,\mathrm{ | + | <center><math>\vec{v}^A_{01}=\vec{\omega}_{01}\times\overrightarrow{OA}=(\dot{\phi}\vec{k}_0)\times(b\,\mathrm{sen}(\theta)\vec{\imath}_0)=b\dot{\phi}\,\mathrm{sen}(\theta)\vec{\jmath}_0</math></center> |
====En el movimiento {21}==== | ====En el movimiento {21}==== | ||
| Línea 67: | Línea 67: | ||
====En el movimiento {01}==== | ====En el movimiento {01}==== | ||
| - | <center><math>\vec{v}^G_{01}=\frac{\vec{v}^A_{01}+\vec{v}^B_{01}}=\frac{b}{2}\dot{\phi}\,\mathrm{ | + | <center><math>\vec{v}^G_{01}=\frac{\vec{v}^A_{01}+\vec{v}^B_{01}}=\frac{b}{2}\dot{\phi}\,\mathrm{sen}(\theta)\vec{\jmath}_0</math></center> |
====En el movimiento {20}==== | ====En el movimiento {20}==== | ||
| - | <center><math>\vec{v}^G_{20}=\frac{\vec{v}^A_{20}+\vec{v}^B_{20}}=\frac{b}{2}\dot{\theta}\left(\cos(\theta)\vec{\imath}_0-\mathrm{ | + | <center><math>\vec{v}^G_{20}=\frac{\vec{v}^A_{20}+\vec{v}^B_{20}}=\frac{b}{2}\dot{\theta}\left(\cos(\theta)\vec{\imath}_0-\mathrm{sen}(\theta)\vec{k}_0\right)</math></center> |
====En el movimiento {21}==== | ====En el movimiento {21}==== | ||
O bien calculamos de nuevo la media o bien, directamente, | O bien calculamos de nuevo la media o bien, directamente, | ||
| - | <center><math>\vec{v}^G_{21}=\vec{v}^G_{20}+\vec{v}^G_{01}=\frac{b}{2}\dot{\theta}\cos(\theta)\vec{\imath}_0\frac{b}{2}\dot{\phi}\,\mathrm{ | + | <center><math>\vec{v}^G_{21}=\vec{v}^G_{20}+\vec{v}^G_{01}=\frac{b}{2}\dot{\theta}\cos(\theta)\vec{\imath}_0\frac{b}{2}\dot{\phi}\,\mathrm{sen}(\theta)\vec{\jmath}_0-\frac{b}{2}\dot{\theta}\,\mathrm{sen}(\theta)\vec{k}_0\right)</math></center> |
===Velocidad angular=== | ===Velocidad angular=== | ||
Revisión de 16:06 2 dic 2020
Contenido |
1 Enunciado
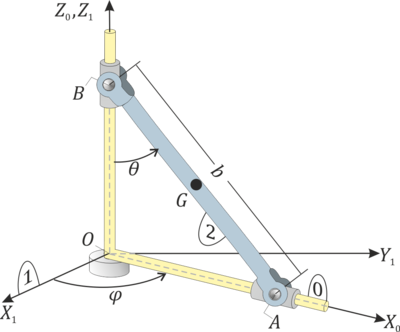
El armazón de barras paralelas a los ejes OX0 y OZ0 (sólido “0”) rota alrededor del eje vertical fijo OZ1, de tal modo que el eje OX0 permanece siempre contenido en el plano horizontal fijo OX1Y1 (sólido “1”). Por otra parte, la varilla AB (sólido “2”), de longitud b, se mueve de forma que su extremo A desliza a lo largo del eje OX0, mientras que su extremo B desliza a lo largo del eje OZ0. Utilizando los ángulos θ y φ (definidos en la figura), así como sus derivadas temporales de primer y segundo orden, determine:
- La velocidad de A, B y G (siendo G el punto medio de la barra) en los movimientos {01}, {20} y {21}, así como la velocidad angular
.
- ¿De qué tipo es el movimiento {21}? ¿Dónde está su EIRMD?
- La aceleración angular
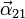y las aceleraciones de A, B y G en los movimientos {01}, {20} y {21}
2 Velocidades
2.1 De B
2.1.1 En el movimiento {01}
Este es el cálculo más fácil. B se halla en el propio eje de rotación de este movimiento, por lo que
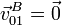
2.1.2 En el movimiento {20}
Esta velocidad la calculamos conjuntamente con la de A, ya que el movimiento de la barra deslizando sobre le eje horizontal y el vertical es idéntico al del “problema de la escalera”.
La velocidad angular de este movimiento es
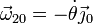
Para sacar el sentido de esta velocidad angular conviene ayudarse de la regla de la mano derecha y ver para donde apunta el pulgar si θ aumenta.
Las velocidades de A y B cumplen
Aplicando el campo de velocidades de un sólido rígido
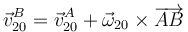
queda
Igualando componente a componente nos queda
En forma vectorial
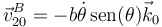
2.1.3 En el movimiento {21}
Una vez que tenemos las dos anteriores, la tercera es inmediata
2.2 De A
2.2.1 En el movimiento {20}
Esta ya le hemos calculado en el apartado anterior
2.2.2 En el movimiento {01}
Esta corresponde a un movimiento de rotación alrededor de OZ1
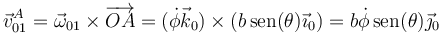
2.2.3 En el movimiento {21}
Por composición de velocidades
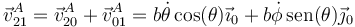
2.3 De G
El punto G es el central entre A y B. Al ser el campo de velocidades una función lineal de la posición el valor en el punto medio es igual a la media de los valores en los extremos. Así tenemos
2.3.1 En el movimiento {01}
2.3.2 En el movimiento {20}
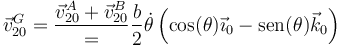
2.3.3 En el movimiento {21}
O bien calculamos de nuevo la media o bien, directamente,
2.4 Velocidad angular
Las velocidades angulares de las dos rotaciones {20} y {01} ya las hemos usado y valen
por lo que la de la composición es
