Entrar Página Discusión Historial Go to the site toolbox

Rotaciones finitas sucesivas de 90° (CMR)

De Laplace

(Diferencias entre revisiones)
(→Primer caso)
Línea 26: Línea 26:
Cuando las rotaciones son de −90° las matrices correspondientes son las inversas, que en el caso de una rotación coinciden con las traspuestas.
Cuando las rotaciones son de −90° las matrices correspondientes son las inversas, que en el caso de una rotación coinciden con las traspuestas.
==Primer caso==
==Primer caso==
 +
===Matriz de rotación===
Si primero giramos en torno a <math>{OY}_1</math> y en segundo lugar alrededor de <math>{OX}_1</math>, ambos del mismo sistema fijo, las matrices deben multiplicarse con la primera rotación a la derecha
Si primero giramos en torno a <math>{OY}_1</math> y en segundo lugar alrededor de <math>{OX}_1</math>, ambos del mismo sistema fijo, las matrices deben multiplicarse con la primera rotación a la derecha
Línea 33: Línea 34:
<center>[[Archivo:rotacion-base-90-01.png|300px]]&nbsp;&nbsp;[[Archivo:rotacion-base-90-02.png|300px]]&nbsp;&nbsp;[[Archivo:rotacion-base-90-03.png|300px]]</center>
<center>[[Archivo:rotacion-base-90-01.png|300px]]&nbsp;&nbsp;[[Archivo:rotacion-base-90-02.png|300px]]&nbsp;&nbsp;[[Archivo:rotacion-base-90-03.png|300px]]</center>
 +
 +
En forma vectorial
 +
<center><math>\begin{array}{ccccc}
 +
\vec{\imath}_3&=&\vec{\jmath}_2&=&\vec{\jmath}_1 \\
 +
\vec{\jmath}_3&=&-\vec{\imath}_2&=&\vec{k}_1 \\
 +
\vec{k}_3&=&\vec{k}_2&=&\vec{\imath}_1
 +
\end{array}</math></center>
 +
 +
===Eje de rotación===
 +
El eje de rotación de este giro compuesto es el autovector que corresponde al autovalor unidad, es decir, cumple
 +
 +
<center><math>\begin{pmatrix}0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0\end{pmatrix}\cdot\begin{pmatrix}u_x\\ u_y\\ u_z\end{pmatrix}= \begin{pmatrix}u_x\\ u_y\\ u_z\end{pmatrix}</math></center>
 +
 +
lo que nos da el sistema
 +
 +
<center><math>u_z=u_x\qquad\qquad u_x=u_y\qquad\qquad u_y=u_z</math></center>
 +
 +
Por tanto, los puntos del eje son aquellos de la forma
 +
 +
<center><math>\overrightarrow{OE}=\lambda(\vec{\imath}_1+\vec{\jmath}_1+\vec{k}_1)</math></center>
 +
 +
Alternativamente, pueden hallarse estos puntos buscando qué vectores tienen las mismas componentes en la base final y la inicial.
 +
===Ángulo girado===
 +
El ángulo girado lo obtenemos analizando qué le ocurre a un vecor perpendicular al eje. Un vector de este tipo puede ser el
 +
<center><math>\vec{A}=\vec{\imath}_1-\vec{\jmath}_1</math></center>
 +
 +
Tras la rotación se transforma en
 +
 +
<center><math>\vec{A}^{\prime}=\begin{pmatrix}0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0\end{pmatrix}\cdot\begin{pmatrix}1\\ -1\\ 0\end{pmatrix}= \begin{pmatrix}0\\ 1\\ -1\end{pmatrix}</math></center>
 +
 +
Alternativamente, puede calcularse el resultado transformando la base
 +
 +
<center><math>\vec{A}^{\prime}=\vec{\imath}_3-\vec{\jmath}_3=\vec{\jmath}_1-\vec{k}_1</math></center>
 +
 +
El ángulo que forma el vector original con el resultado de la rotación lo da
 +
 +
<center><math>\cos(\theta)=\frac{\vec{A}\cdot\vec{A}^\prime}{|\vec{A}|\,|\vec{A}^\prime|}=-\frac{1}{2}</math></center>
 +
 +
luego el ánguko girado es 120°.
==Segundo caso==
==Segundo caso==
==Tercer caso==
==Tercer caso==
==Cuarto caso==
==Cuarto caso==

Revisión de 19:26 28 nov 2020

Contenido

1 Enunciado

Se tiene un sólido situado de tal manera que inicialmente los sistemas de referencia fijo, “1” y ligado, “2”, coinciden.

  1. Supongamos que el sólido se hace girar en primer lugar +90° en torno a OY1 y a continuación +90° en torno a OX1. ¿Cuál es la matriz de rotación que permite pasar de las coordenadas (X,Y,Z) en la posición final del sistema ligado a las coordenadas en el sistema fijo (x,y,z)? ¿Cuál es el eje de rotación de la composición? ¿Cuál es el ángulo girado?
  2. ¿Cómo cambian los resultados anteriores si, partiendo de la posición inicial se hace girar en primer lugar +90° en torno a OX1 y a continuación +90° en torno a OY1?
  3. ¿Cómo cambian los resultados anteriores si, partiendo de la posición inicial se hace girar en primer lugar +90° en torno a OY1 y a continuación +90° en torno a OX2?
  4. Si se realizan las dos rotaciones del apartado (a) (1º +90° en torno a OY1; 2º +90° en torno a OX1) y a continuación se gira −90° en torno a OY1 seguido de −90° en torno a OX1, ¿vuelve el sólido a su posición inicial? Si no es así, ¿cuál es el eje de rotación y el ángulo girado?

2 Introducción

En este problema tenemos una sucesión de rotaciones de 90°. Estas relaciones se pueden analizar viendo como se transforman las bases o mediante métodos matriciales.

En general, para una rotación alrededor del eje OX tenemos la siguiente matriz de rotación que nos da las coordenadas en el sistema dijo partiendo de las que tiene en el sistema ligado

R_x(\phi)=\begin{pmatrix}1 & 0 & 0 \\ 0 & \cos(\phi) & -\mathrm{sen}(\phi) \\ 0 & \mathrm{sen}(\phi) & \cos(\phi)\end{pmatrix}

Para una rotación en torno a OY

R_y(\phi)=\begin{pmatrix} \cos(\phi) & 0 & \mathrm{sen}(\phi) \\ 0 & 1 & 0 \\ -\mathrm{sen}(\phi) & 0 & \cos(\phi)\end{pmatrix}

y para una en torno a OZ

R_z(\phi)=\begin{pmatrix} \cos(\phi) & -\mathrm{sen}(\phi) & 0 \\ \mathrm{sen}(\phi) & \cos(\phi) & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}

En el caso particular de rotaciones de +90°, esta matrices se reducen a

R_x=\begin{pmatrix}1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0\end{pmatrix}\qquad\qquad R_y=\begin{pmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ -1 & 0 & 0\end{pmatrix}\qquad\qquad R_z=\begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}

Cuando las rotaciones son de −90° las matrices correspondientes son las inversas, que en el caso de una rotación coinciden con las traspuestas.

3 Primer caso

3.1 Matriz de rotación

Si primero giramos en torno a OY1 y en segundo lugar alrededor de OX1, ambos del mismo sistema fijo, las matrices deben multiplicarse con la primera rotación a la derecha

R=R_x\cdot R_y = \begin{pmatrix}1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0\end{pmatrix}\cdot\begin{pmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ -1 & 0 & 0\end{pmatrix} =\begin{pmatrix}0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0\end{pmatrix}

Gráficamente, podemos ver que transformación de las bases es la siguiente. La primera rotación lleva de la base 1 a la 2, y la 2ª de la 2 a la 3.

    

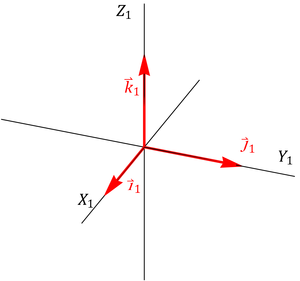
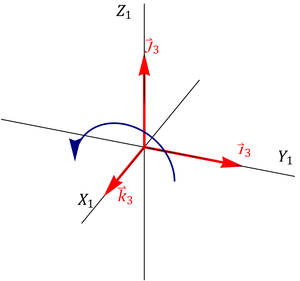
En forma vectorial

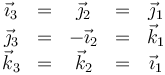
\begin{array}{ccccc} \vec{\imath}_3&=&\vec{\jmath}_2&=&\vec{\jmath}_1 \\ \vec{\jmath}_3&=&-\vec{\imath}_2&=&\vec{k}_1 \\ \vec{k}_3&=&\vec{k}_2&=&\vec{\imath}_1 \end{array}

3.2 Eje de rotación

El eje de rotación de este giro compuesto es el autovector que corresponde al autovalor unidad, es decir, cumple

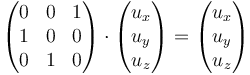
\begin{pmatrix}0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0\end{pmatrix}\cdot\begin{pmatrix}u_x\\ u_y\\ u_z\end{pmatrix}= \begin{pmatrix}u_x\\ u_y\\ u_z\end{pmatrix}

lo que nos da el sistema

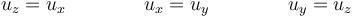
u_z=u_x\qquad\qquad u_x=u_y\qquad\qquad u_y=u_z

Por tanto, los puntos del eje son aquellos de la forma

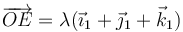
\overrightarrow{OE}=\lambda(\vec{\imath}_1+\vec{\jmath}_1+\vec{k}_1)

Alternativamente, pueden hallarse estos puntos buscando qué vectores tienen las mismas componentes en la base final y la inicial.

3.3 Ángulo girado

El ángulo girado lo obtenemos analizando qué le ocurre a un vecor perpendicular al eje. Un vector de este tipo puede ser el

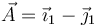
\vec{A}=\vec{\imath}_1-\vec{\jmath}_1

Tras la rotación se transforma en

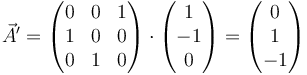
\vec{A}^{\prime}=\begin{pmatrix}0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0\end{pmatrix}\cdot\begin{pmatrix}1\\ -1\\ 0\end{pmatrix}= \begin{pmatrix}0\\ 1\\ -1\end{pmatrix}

Alternativamente, puede calcularse el resultado transformando la base

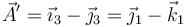
\vec{A}^{\prime}=\vec{\imath}_3-\vec{\jmath}_3=\vec{\jmath}_1-\vec{k}_1

El ángulo que forma el vector original con el resultado de la rotación lo da

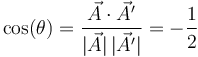
\cos(\theta)=\frac{\vec{A}\cdot\vec{A}^\prime}{|\vec{A}|\,|\vec{A}^\prime|}=-\frac{1}{2}

luego el ánguko girado es 120°.

4 Segundo caso

5 Tercer caso

6 Cuarto caso

Obtenido de "http://tesla.us.es/wiki/index.php/Rotaciones_finitas_sucesivas_de_90%C2%B0_(CMR)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace