Rotaciones finitas sucesivas de 90° (CMR)
De Laplace
Contenido |
1 Enunciado
Se tiene un sólido situado de tal manera que inicialmente los sistemas de referencia fijo, “1” y ligado, “2”, coinciden.
- Supongamos que el sólido se hace girar en primer lugar +90° en torno a OY1 y a continuación +90° en torno a OX1. ¿Cuál es la matriz de rotación que permite pasar de las coordenadas (X,Y,Z) en la posición final del sistema ligado a las coordenadas en el sistema fijo (x,y,z)? ¿Cuál es el eje de rotación de la composición? ¿Cuál es el ángulo girado?
- ¿Cómo cambian los resultados anteriores si, partiendo de la posición inicial se hace girar en primer lugar +90° en torno a OX1 y a continuación +90° en torno a OY1?
- ¿Cómo cambian los resultados anteriores si, partiendo de la posición inicial se hace girar en primer lugar +90° en torno a OY1 y a continuación +90° en torno a OX2?
- Si se realizan las dos rotaciones del apartado (a) (1º +90° en torno a OY1; 2º +90° en torno a OX1) y a continuación se gira −90° en torno a OY1 seguido de −90° en torno a OX1, ¿vuelve el sólido a su posición inicial? Si no es así, ¿cuál es el eje de rotación y el ángulo girado?
2 Introducción
En este problema tenemos una sucesión de rotaciones de 90°. Estas relaciones se pueden analizar viendo como se transforman las bases o mediante métodos matriciales.
En general, para una rotación alrededor del eje OX tenemos la siguiente matriz de rotación que nos da las coordenadas en el sistema dijo partiendo de las que tiene en el sistema ligado
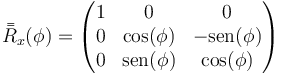
Para una rotación en torno a OY
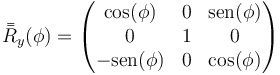
y para una en torno a OZ
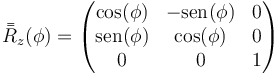
En el caso particular de rotaciones de +90°, esta matrices se reducen a
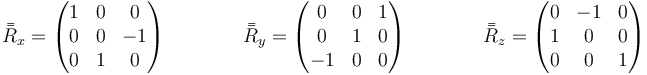
Cuando las rotaciones son de −90° las matrices correspondientes son las inversas, que en el caso de una rotación coinciden con las traspuestas.
3 Primer caso
3.1 Matriz de rotación
Si primero giramos en torno a OY1 y en segundo lugar alrededor de OX1, ambos del mismo sistema fijo, las matrices deben multiplicarse con la primera rotación a la derecha
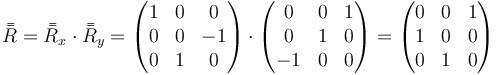
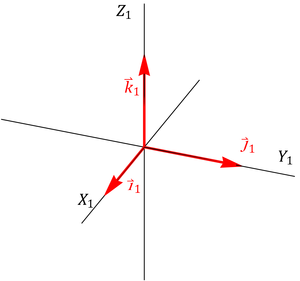
Gráficamente, podemos ver que transformación de las bases es la siguiente. La primera rotación lleva de la base 1 a la 2, y la 2ª de la 2 a la 3.

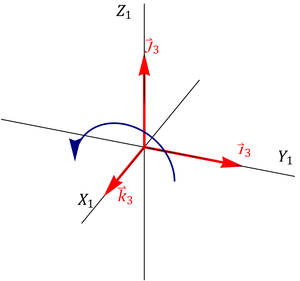
En forma vectorial
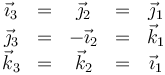
3.2 Eje de rotación
El eje de rotación de este giro compuesto es el autovector que corresponde al autovalor unidad, es decir, cumple
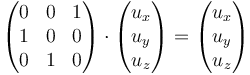
lo que nos da el sistema
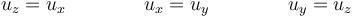
Por tanto, los puntos del eje son aquellos de la forma
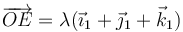
Alternativamente, pueden hallarse estos puntos buscando qué vectores tienen las mismas componentes en la base final y la inicial.
3.3 Ángulo girado
El ángulo girado lo obtenemos analizando qué le ocurre a un vector perpendicular al eje. Un vector de este tipo puede ser el
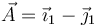
Tras la rotación se transforma en
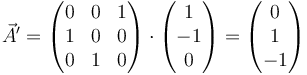
Alternativamente, puede calcularse el resultado transformando la base
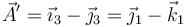
El ángulo que forma el vector original con el resultado de la rotación lo da
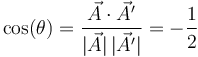
luego el ángulo girado es 120°.
4 Segundo caso
4.1 Matriz de rotación
En el segundo caso, se efectúan las mismas dos rotaciones, pero en orden inverso. En ese caso, el producto de las dos matrices no da el mismo resultado
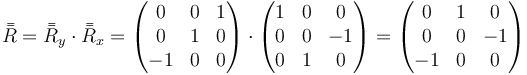
Gráficamente, la relación entre bases

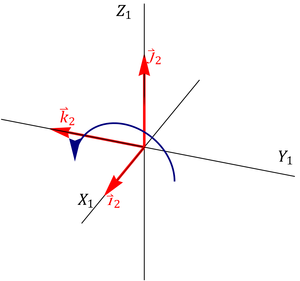

En forma vectorial
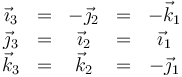
4.2 Eje de rotación
El eje de rotación de este giro compuesto es el autovector que corresponde al autovalor unidad
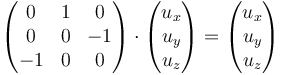
lo que nos da
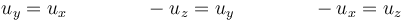
Por tanto, los puntos del eje son aquellos de la forma
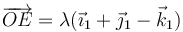
Alternativamente, pueden hallarse estos puntos buscando qué vectores tienen las mismas componentes en la base final y la inicial.
4.3 Ángulo girado
El ángulo girado lo obtenemos analizando qué le ocurre a un vector perpendicular al eje. Un vector de este tipo puede ser el
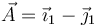
Tras la rotación se transforma en
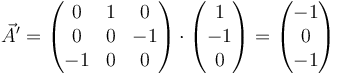
Alternativamente, puede calcularse el resultado transformando la base
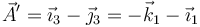
El ángulo que forma el vector original con el resultado de la rotación lo da
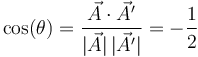
luego el ángulo girado es de nuevo 120°, pero alrededor de un eje distinto.
5 Tercer caso
El tercer caso parece una repetición del primero, pero en realidad es una copia del segundo. La razón es que el segundo giro se produce en torno al eje OX2 (es decir, el resultado de la primera rotación) en lugar del OX1. En ese caso el ordenamiento de las matrices se hace de izquierda a derecha
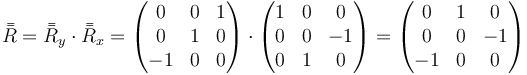
Gráficamente, se puede observar cómo el resultado final es el mismo que en el caso anterior, pero no así el estado intermedio. Vemos que el segundo giro se produce alrededor de 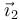 ,
,



En forma vectorial
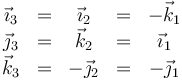
El eje de rotación y el ángulo girado son, lógicamente, los mismos que en el apartado anterior.
Obsérvese que, si este proceso lo consideramos como una rotación sucesiva en torno a los ejes fijos, la segunda es una de +90° en torno a 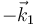 o, lo que es lo mismo, una de −90° en torno a
o, lo que es lo mismo, una de −90° en torno a 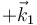 . En ese caso calcularíamos la matriz de la composición como
. En ese caso calcularíamos la matriz de la composición como
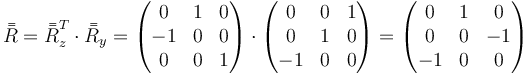
6 Cuarto caso
6.1 Matriz de rotación
En el cuarto caso, parecería que al hacer dos rotaciones en un sentido y dos en el opuesto sus efectos se anularían, pero no es así, ya que el oren es importante.
as matrices correspondientes a las rotaciones inversas, de −90° son las traspuestas de las originales. Por tanto, la matriz resultante es
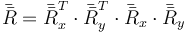
lo que da
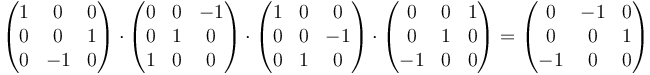
Gráficamente




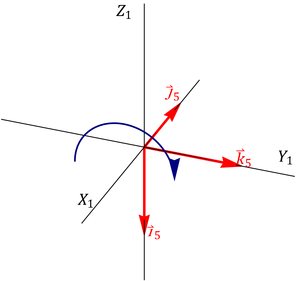
En forma vectorial
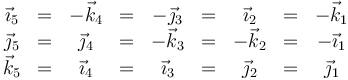
6.2 Eje de rotación
El eje de rotación es la solución de la ecuación
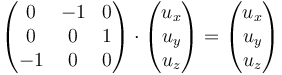
es decir
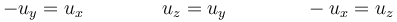
Por tanto, los puntos del eje son aquellos de la forma
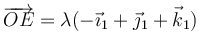
6.3 Ángulo girado
Como en los casos anteriores, el ángulo girado es de 120°





