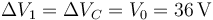Circuito con resistencias, condensador y bobina

De Laplace

Revisión de 08:53 5 may 2020

1 Enunciado

Se tiene el circuito de la figura, en el cual hay tres resistencias, un condensador y una bobina y autoinducción. Todo el conjunto está conectado a una diferencia de potencial .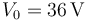

En el sistema hay situados dos amperímetros y dos voltímetros. ¿Qué marcará cada uno de estos aparatos de medida?

2 Solución

En el circuito, los amperímetros y voltímetros no afectan a las corrientes y voltajes, solo los miden. Desde el punto de vista del circuito, un amperímetro es un cortocircuito (no hay d.d.p. entre sus extremos) y voltímetro funciona como un circuito abierto (la intensidad de corriente por su interior es nula).

Tenemos tres ramas en paralelo, que etiquetaremos respectivamente como “a”, “b” y “c”. Al estar en paralelo están simetidas a la misma diferencia de potencial, que en este caso es la tensión que fija la fuente.

Veamos cada rama por separado.

2.1 Rama superior

La rama superior (“a”) está formado por dos elementos en serie: una resistencia y un condensador. Por estar en serie, la d.d.p. total es la suma de las respectivas.

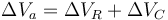
siendo

Ahora bien, toda la corriente que circula por esta resistencia va a parar al condensador, por lo que, por la ley de conservación de la carga

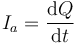
En una situación de corriente continua todas las cantidades son constantes y por tanto

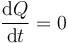
lo que nos dice que la intensidad de corriente que circula por esta rama es nula

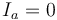
es decir, el condensador se comporta como un circuito abierto en corriente continua. Impide el paso de la corriente por esa rama.

Si la corriente es nula también lo es la d.d.p. en esa resistencia

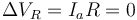
y por tanto, toda el voltaje de esa rama cae en el condensador

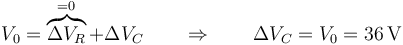
Esta es justamente la lectura del voltímetro 1, que está conectado a las placas o armaduras del condensador