Campo de dos discos paralelos (GIOI)
De Laplace
(Página creada con '==Enunciado== Se tienen dos discos de radio 1cm y con cargas respectivas de ±12 nC situados paralelamente al plano OXY, con sus centros en <math>(±b/2) \vec{k}</math>. Halle…') |
|||
| Línea 5: | Línea 5: | ||
# {{nivel|3}} <math>b</math> tiene un valor arbitrario. Estime el error cometido en los dos apartados anteriores. | # {{nivel|3}} <math>b</math> tiene un valor arbitrario. Estime el error cometido en los dos apartados anteriores. | ||
| - | ==Distancia | + | ==Distancia 1 m== |
| - | ==Distancia | + | En el primer caso tenemos que los dos discos están muy alejados de la posición donde queremos hallar el campo, por lo que podemos hacer la aproximación de que se ven como [[Campo_de_dos_cargas_puntuales_(GIOI)|cargas puntuales]]. |
| + | |||
| + | En ese caso, el campo que crea cada una de ellas en la posición central es el mismo, por lo que el campo total será el doble del que crea cada disco (el disco positivo crea un campo que va hacia la negativa, y el disco negativo lo mismo) | ||
| + | |||
| + | <center><math>\vec{E}=\vec{E}_1+\vec{E}_2=2\vec{E}_1</math></center> | ||
| + | |||
| + | siendo el campo aproximado de cada disco, en N/C | ||
| + | |||
| + | <center><math>\vec{E}_1=\frac{1}{4\pi\varepsilon_0}\,\frac{Q}{(b/2)^2}\vec{k}=9\times 10^9\,\frac{12\times 10^-9}{0.5^2}\vec{k}=432\vec{k}</math></center> | ||
| + | |||
| + | y el campo total | ||
| + | |||
| + | <center><math>\vec{E}=2\vec{E}_1=864\vec{k}</math></center> | ||
| + | ==Distancia 1 mm== | ||
| + | En el segundo caso, al estar los planos muy próximos, se ven muy grandes, con lo que podemos hacer la aproximación de campo como el de [[Campo_de_dos_planos_paralelos_(GIOI)|dos planos paralelos]] infinitos. En ese caso, el campo aproximado es | ||
| + | |||
| + | <center><math>\vec{E}=\frac{\sigma_s}{\varepsilon_0}\vec{k}=\frac{Q/(\pi R^2)}{\varepsilon_0 }\vec{k}=\frac{4Q}{4\pi\varepsilon_0 R^2}\vec{k}</math></center> | ||
| + | |||
| + | con el valor numérico, en N/C | ||
| + | |||
| + | <center><math>\vec{E}=9\times 10^9 \frac{4\times 12\times 10^-9}{0.01^2}\vec{k}=4.42\times 10^6\vec{k}</math></center> | ||
==Resultado exacto== | ==Resultado exacto== | ||
| + | El valor exacto lo obtenemos aplicando el resultado del [[Campo_de_un_disco_homogéneo_(GIOI)|campo creado por un disco]] | ||
| + | |||
| + | <center><math>\vec{E}=2\vec{E}_1 = \frac{2Q}{2\pi\varepsilon_0 R^2}\left(1-\frac{b/2}{\sqrt{(b/2)^2+R^2}}}\right)\vec{k}=\frac{4Q}{4\pi\varepsilon_0 R^2}\left(1-\frac{b}{\sqrt{b^2+4R^2}}}\right)\vec{k}</math></center> | ||
| + | |||
| + | |||
==Estimación del error== | ==Estimación del error== | ||
Revisión de 17:35 17 feb 2020
Contenido |
1 Enunciado
Se tienen dos discos de radio 1cm y con cargas respectivas de ±12 nC situados paralelamente al plano OXY, con sus centros en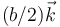 
. Halle el valor aproximado del campo eléctrico en el origen de coordenadas si:
-
b = 1m.
-
.
-
b tiene un valor arbitrario. Estime el error cometido en los dos apartados anteriores.
2 Distancia 1 m
En el primer caso tenemos que los dos discos están muy alejados de la posición donde queremos hallar el campo, por lo que podemos hacer la aproximación de que se ven como cargas puntuales.
En ese caso, el campo que crea cada una de ellas en la posición central es el mismo, por lo que el campo total será el doble del que crea cada disco (el disco positivo crea un campo que va hacia la negativa, y el disco negativo lo mismo)
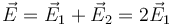
siendo el campo aproximado de cada disco, en N/C
y el campo total
3 Distancia 1 mm
En el segundo caso, al estar los planos muy próximos, se ven muy grandes, con lo que podemos hacer la aproximación de campo como el de dos planos paralelos infinitos. En ese caso, el campo aproximado es
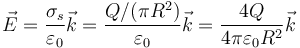
con el valor numérico, en N/C
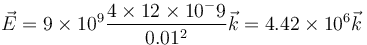
4 Resultado exacto
El valor exacto lo obtenemos aplicando el resultado del campo creado por un disco
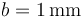