Entrar Página Discusión Historial Go to the site toolbox

Movimiento de una mancuerna ideal

De Laplace

(Diferencias entre revisiones)
Antonio (Discusión | contribuciones)
(Página creada con '==Enunciado== Supongamos dos masas iguales ''m'' unidas por una barra rígida de longitud ''b'', sin masa (lo que sería una mancuerna ideal). Las masas reposan sobre un plano h…')

última version al 13:27 6 ene 2020

Contenido

1 Enunciado

Supongamos dos masas iguales m unidas por una barra rígida de longitud b, sin masa (lo que sería una mancuerna ideal). Las masas reposan sobre un plano horizontal, sobre el que pueden moverse sin rozamiento. A una de las masas se le comunica una velocidad inicial \vec{v}_0 perpendicular a la línea de la barra, mientras que la otra se encuentra inicialmente en reposo. ¿Cuánto valen la cantidad de movimiento, el momento cinético respecto al CM y la energía cinética de la barra? ¿Cómo es el movimiento del sistema a partir de ese momento?

2 Cantidad de movimiento

La cantidad de movimiento del sistema es la suma de los de las partículas que lo componen

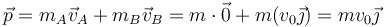
\vec{p}=m_A\vec{v}_A+m_B\vec{v}_B=m\cdot \vec{0}+m(v_0\vec{\jmath})=mv_0\vec{\jmath}

Esto nos da la velocidad del CM

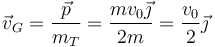
\vec{v}_G=\frac{\vec{p}}{m_T}=\frac{mv_0\vec{\jmath}}{2m}=\frac{v_0}{2}\vec{\jmath}

3 Momento cinético

3.1 Respecto al CM

El momento cinético respecto al CM lo podemos calcular considerando el CM como un punto fijo o como un punto móvil. En ambos casos el resultado es el mismo.

3.1.1 Como un punto fijo

La expresión es

\vec{L}_G=m_A\overrightarrow{GA}\times\vec{v}_A+m_B\overrightarrow{GB}\times\vec{v}_B=m\left(-\frac{b}{2}\vec{\imath}\right)\times \vec{0}+m\left(\frac{b}{2}\vec{\imath}\right)\times (v_0\vec{\jmath})=\frac{mbv_0}{2}\vec{k}

3.1.2 Como punto móvil

Alternativamente, podemos calcular primero las velocidades respecto al CM

\vec{v}^{\prime}_A=\vec{v}_A-\vec{v}_G=-\frac{v_0}{2}\vec{\jmath}\qquad\qquad \vec{v}^{\prime}_B=\vec{v}_B-\vec{v}_G=+\frac{v_0}{2}\vec{\jmath}

y calcular el momento cinético empleando estas velocidades

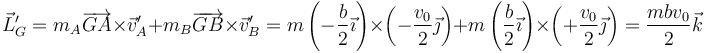
\vec{L}^{\prime}_G=m_A\overrightarrow{GA}\times\vec{v}^{\prime}_A+m_B\overrightarrow{GB}\times\vec{v}^{\prime}_B=m\left(-\frac{b}{2}\vec{\imath}\right)\times \left(-\frac{v_0}{2}\vec{\jmath}\right)+m\left(\frac{b}{2}\vec{\imath}\right)\times \left(+\frac{v_0}{2}\vec{\jmath}\right)=\frac{mbv_0}{2}\vec{k}

3.1.3 Empleando el momento de inercia

Alternativamente, puede calcularse el momento cinético como

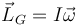
\vec{L}_G=I\vec{\omega}

El momento de inercia respecto a un eje perpendicular a la varilla por el CM es

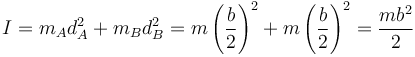
I=m_A d_A^2+m_B d_B^2 = m\left(\frac{b}{2}\right)^2+m\left(\frac{b}{2}\right)^2=\frac{mb^2}{2}

y la velocidad angular la sacamos de

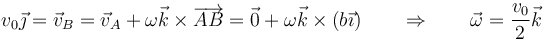
v_0\vec{\jmath}=\vec{v}_B=\vec{v}_A+\omega\vec{k}\times\overrightarrow{AB}=\vec{0}+\omega \vec{k}\times(b\vec{\imath})\qquad\Rightarrow\qquad \vec{\omega}=\frac{v_0}{2}\vec{k}

Resulta el momento cinético

\vec{L}_G=I\vec{\omega}=\left(\frac{mb^2}{2}\right) \left(\frac{v_0}{2}\vec{k}\right)=\frac{mbv_0}{2}\vec{k}

3.2 Respecto a un punto fijo

Para cualquier otro punto, puede hallarse a partir de la suma de los de las dos masas

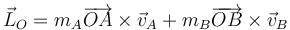
\vec{L}_O=m_A\overrightarrow{OA}\times\vec{v}_A+m_B\overrightarrow{OB}\times\vec{v}_B

o bien empleando el teorema de König

\vec{L}_O=m_T\overrightarrow{OG}\times\vec{v}_G+\vec{L}_G\qquad\qquad (m_T=2m)

Así, para el propio extremo A,

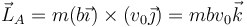
\vec{L}_A=m(b\vec{\imath})\times(v_0\vec{\jmath})=mbv_0\vec{k}

Empleando aquí el teorema de König

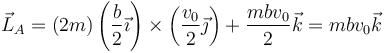
\vec{L}_A=(2m)\left(\frac{b}{2}\vec{\imath}\right)\times\left(\frac{v_0}{2}\vec{\jmath}\right)+\frac{mbv_0}{2}\vec{k}=mbv_0\vec{k}

4 Energía cinética

La energía cinética la podemos hallar a partir de las de las partículas

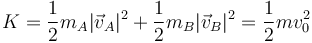
K=\frac{1}{2}m_A|\vec{v}_A|^2+\frac{1}{2}m_B|\vec{v}_B|^2=\frac{1}{2}mv_0^2

o empleando el teorema de König

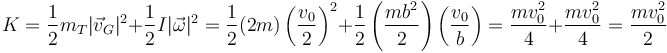
K=\frac{1}{2}m_T|\vec{v}_G|^2+\frac{1}{2}I|\vec{\omega}|^2=\frac{1}{2}(2m)\left(\frac{v_0}{2}\right)^2+\frac{1}{2}\left(\frac{mb^2}{2}\right)\left(\frac{v_0}{b}\right)=\frac{mv_0^2}{4}+\frac{mv_0^2}{4}=\frac{mv_0^2}{2}

Vemos que en este caso la energía se reparte mitad y mitad en traslación y rotación.

También se puede hallar la energía cinética a partir de la cantidad de movimiento y del momento cinético

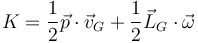
K=\frac{1}{2}\vec{p}\cdot\vec{v}_G+\frac{1}{2}\vec{L}_G\cdot\vec{\omega}

Esta expresión se puede aplicar respecto a cualquier punto, no solo el CM. Así, empleando el punto AB

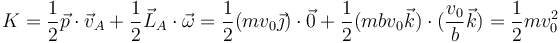
K=\frac{1}{2}\vec{p}\cdot\vec{v}_A+\frac{1}{2}\vec{L}_A\cdot\vec{\omega}=\frac{1}{2}(mv_0\vec{\jmath})\cdot\vec{0}+\frac{1}{2}(mbv_0\vec{k})\cdot(\frac{v_0}{b}\vec{k})=\frac{1}{2}mv_0^2

5 Movimiento posterior

Si no hay ninguna fuerza actuando sobre el sistema, se conserva la cantidad de movimiento y el momento cinético (y, por tanto, la energía cinética).

Esto implica que la velocidad del CM permanece constante, describiendo un movimiento rectilíneo y uniforme.

La velocidad angular también permanece constante, por lo que la varilla gira uniformemente.

El resultado, para cada una de las masas, es que el movimiento es una combinación de rotación y traslación, resultando un movimiento cicloidal.

Imagen:barrarotante.gif
Obtenido de "http://tesla.us.es/wiki/index.php/Movimiento_de_una_mancuerna_ideal"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 13:27, 6 ene 2020. - Esta página ha sido visitada 385 veces. - Aviso legal - Acerca de Laplace