Entrar Página Discusión Historial Go to the site toolbox

Problemas de cinemática del sólido rígido (GIOI)

De Laplace

(Diferencias entre revisiones)
Línea 23: Línea 23:
[[Movimiento de un sólido conocido un eje|Solución]]
[[Movimiento de un sólido conocido un eje|Solución]]
 +
 +
==Rapidez de los puntos de un tornillo==
 +
Un tornillo de radio 2 mm y paso de rosca 1 mm avanza impulsado por un destornillador de forma que su punta se mueve a 2 mm/s. Determine la rapidez de los puntos del filete del tornillo.
 +
 +
<center>[[Archivo:tornillo.png]]</center>
 +
 +
[[Rapidez de los puntos de un tornillo|Solución]]
 +
 +
==Rodadura y deslizamiento de un disco==
 +
Un disco de radio <math>R</math> y masa <math>M</math> rueda y desliza sobre el plano horizontal <math>y=0</math> de forma que la velocidad del punto de contacto con el suelo, A, y del diametralmente opuesto, B son de la forma
 +
 +
<center><math>\vec{v}_A = v_A\vec{\imath}\qquad \vec{v}_B = v_B\vec{\imath}</math></center>
 +
 +
# Calcule la velocidad angular del disco.
 +
# Halle la velocidad del centro del disco, C, así como de los puntos D y E situados en los extremos de un diámetro horizontal.
 +
# Determine la posición del centro instantáneo de rotación.
 +
# Indique a qué se reducen los resultados anteriores en los casos particulares siguientes:
 +
## <math>v_A = -v_B</math>
 +
## <math>v_A = 0</math>
 +
## <math>v_A = v_B</math>
 +
 +
[[Rodadura y deslizamiento de un disco|Solución]]
 +
 +
==Movimiento de un sistema biela-manivela==
 +
Un sistema biela-manivela está formado por: una barra fija (el ''eje'' &ldquo;1&rdquo;); una barra (la ''manivela'' &ldquo;0&rdquo;) de longitud <math>L</math>, articulada en el punto O del eje y que forma un ángulo <math>\theta(t)</math> con él; y una segunda barra
 +
(la ''biela'' &ldquo;2&rdquo;), también de longitud <math>L</math>, articulada en el punto A de la manivela y cuyo segundo extremo B está obligado a deslizar por el eje.
 +
 +
<center>[[Archivo:esquema-biela-manivela.png]]</center>
 +
 +
# Halle las velocidades de los puntos A y B de la biela.
 +
# Determine la velocidad angular de la biela respecto al eje.
 +
# Localice el centro instantáneo de rotación (CIR) de la biela respecto al eje.
 +
# Suponga el caso <math>L=50\,\mathrm{cm}</math> y que en un instante dado <math>\mathrm{tg}(\theta)=0.75</math> siendo <math>\dot{\theta}=-2.00\,\mathrm{rad}/\mathrm{s}</math>. Calcule la velocidades respecto al eje de los puntos A y B de la biela, su velocidad angular y las coordenadas del CIR.
 +
 +
[[Movimiento de un sistema biela-manivela|Solución]]
 +
 +
==Diferentes movimientos de una esfera==
 +
Considérese una esfera de masa <math>M</math> y radio <math>R</math> que se mueve sobre la superficie horizontal <math>z=0</math>. Consideramos un instante en el que la esfera toca el suelo justo en el origen de coordenadas, O, y tal que en ese momento la velocidad de
 +
dicho punto de contacto con el suelo es nula
 +
 +
<center><math>\vec{v}_O = \vec{0}</math></center>
 +
 +
Para este mismo instante la velocidad de los puntos <math>\vec{r}_A=-R\vec{\imath}+R\vec{k}</math> y <math>\vec{r}_B=+R\vec{\imath}+R\vec{k}</math> situados en un diámetro horizontal valen respectivamente
 +
 +
<center><math>\vec{v}_A = v_A\vec{\jmath}\qquad \vec{v}_B = v_B\vec{\jmath}</math></center>
 +
 +
Para los tres casos siguientes:
 +
 +
* <math>v_A=+v_B</math>
 +
* <math>v_A=0</math>
 +
* <math>v_A=-v_B</math>
 +
 +
# Indique justificadamente el tipo de movimiento instantáneo que realiza la esfera (traslación, rotación, helicoidal,&hellip;)
 +
# Calcule la velocidad angular del sólido.
 +
# Halle la velocidad angular de pivotamiento y la de rodadura de la esfera.
 +
# Dé la ecuación del eje instantáneo de rotación y mínimo deslizamiento (o de rotación, en su caso).
 +
# Calcule la velocidad lineal del centro C de la esfera y la del punto D situado en el extremo superior de la esfera.
 +
 +
[[Diferentes movimientos de una esfera|Solución]]
 +
 +
==Rodadura y pivotamiento de una esfera==
 +
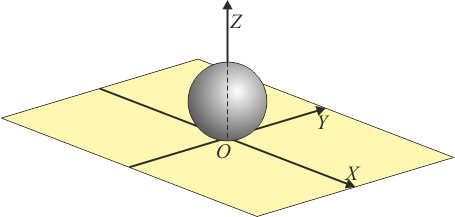
Una esfera maciza de 2.5&thinsp;cm de radio y 0.400&thinsp;kg de masa rueda y pivota sin deslizar sobre una superficie horizontal. En un instante dado la velocidad angular de pivotamiento es de 1.80&thinsp;rad/s en sentido antihorario respecto al eje OZ (tomando como origen el punto de contacto y como eje OZ el perpendicular al plano), mientras que la de rodadura es de 2.40&thinsp;rad/s en la dirección del vector unitario
 +
 +
<center><math>\vec{u}=0.80\vec{\imath}+0.60\vec{\jmath}</math></center>
 +
 +
Para este instante, calcule:
 +
# El vector velocidad angular y la ecuación del eje instantáneo de rotación.
 +
# La velocidad y la rapidez del centro de la esfera.
 +
# La distancia del centro de la esfera al eje instantáneo de rotación.
 +
# La cantidad de movimiento, el momento cinético y la energía cinética de la esfera.
 +
 +
'''Dato:''' Momento de inercia de una esfera respecto a un eje que pasa por su centro <math>I=(2/5)MR^2</math>.
 +
 +
<center>[[Archivo:bola-sobre-plano.png]]</center>
 +
 +
[[Rodadura y pivotamiento de una esfera|Solución]]

Revisión de 13:47 16 dic 2019

Contenido

1 Caso de campo de velocidades de un sólido

El campo de velocidades instantáneo de un sólido rígido tiene la expresión, en el sistema internacional

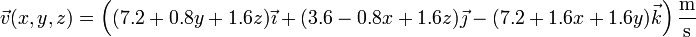
\vec{v}(x,y,z)=\left((7.2 + 0.8 y + 1.6 z)\vec{\imath}+(3.6 - 0.8 x + 1.6 z)\vec{\jmath} -(7.2+1.6 x+1.6 y)\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}}
  1. Determine la velocidad angular, \vec{\omega}, y la velocidad del origen de coordenadas, \vec{v}_0.
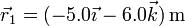  2. Halle la velocidad del punto \vec{r}_1=(-5.0\vec{\imath}-6.0\vec{k})\,\mathrm{m}.
  3. ¿Qué tipo de movimiento describe el sólido en este instante?
  4. Halle la ecuación del eje instantáneo de rotación y mínimo deslizamiento (o eje instantáneo de rotación, en su caso).

Solución

2 Movimiento de un sólido conocido un eje

Un sólido rígido se encuentra en rotación instantánea alrededor de un eje que pasa por el punto A(1,0, − 1) y lleva la dirección del vector 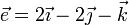\vec{e}=2\vec{\imath}-2\vec{\jmath}-\vec{k}, de tal forma que la velocidad del punto B(0,2,1) es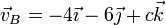 \vec{v}_B=-4\vec{\imath}-6\vec{\jmath}+c\vec{k}

  1. Halle el valor de la constante c.
  2. Calcule la velocidad angular instantánea.
  3. Calcule la velocidad del punto P(1,1,0).

Todas las cantidades están expresadas en las unidades del SI.

Solución

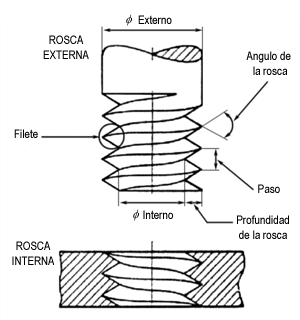
3 Rapidez de los puntos de un tornillo

Un tornillo de radio 2 mm y paso de rosca 1 mm avanza impulsado por un destornillador de forma que su punta se mueve a 2 mm/s. Determine la rapidez de los puntos del filete del tornillo.

Archivo:tornillo.png

Solución

4 Rodadura y deslizamiento de un disco

Un disco de radio R y masa M rueda y desliza sobre el plano horizontal y = 0 de forma que la velocidad del punto de contacto con el suelo, A, y del diametralmente opuesto, B son de la forma

\vec{v}_A = v_A\vec{\imath}\qquad \vec{v}_B = v_B\vec{\imath}
  1. Calcule la velocidad angular del disco.
  2. Halle la velocidad del centro del disco, C, así como de los puntos D y E situados en los extremos de un diámetro horizontal.
  3. Determine la posición del centro instantáneo de rotación.
  4. Indique a qué se reducen los resultados anteriores en los casos particulares siguientes:
    1. vA = − vB
    2. vA = 0
    3. vA = vB

Solución

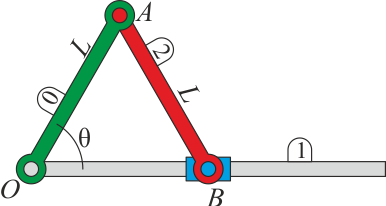
5 Movimiento de un sistema biela-manivela

Un sistema biela-manivela está formado por: una barra fija (el eje “1”); una barra (la manivela “0”) de longitud L, articulada en el punto O del eje y que forma un ángulo θ(t) con él; y una segunda barra (la biela “2”), también de longitud L, articulada en el punto A de la manivela y cuyo segundo extremo B está obligado a deslizar por el eje.

Archivo:esquema-biela-manivela.png
  1. Halle las velocidades de los puntos A y B de la biela.
  2. Determine la velocidad angular de la biela respecto al eje.
  3. Localice el centro instantáneo de rotación (CIR) de la biela respecto al eje.
  4. Suponga el caso 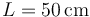L=50\,\mathrm{cm} y que en un instante dado tg(θ) = 0.75 siendo 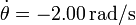\dot{\theta}=-2.00\,\mathrm{rad}/\mathrm{s}. Calcule la velocidades respecto al eje de los puntos A y B de la biela, su velocidad angular y las coordenadas del CIR.

Solución

6 Diferentes movimientos de una esfera

Considérese una esfera de masa M y radio R que se mueve sobre la superficie horizontal z = 0. Consideramos un instante en el que la esfera toca el suelo justo en el origen de coordenadas, O, y tal que en ese momento la velocidad de dicho punto de contacto con el suelo es nula

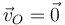
\vec{v}_O = \vec{0}

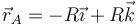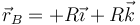Para este mismo instante la velocidad de los puntos \vec{r}_A=-R\vec{\imath}+R\vec{k} y \vec{r}_B=+R\vec{\imath}+R\vec{k} situados en un diámetro horizontal valen respectivamente

\vec{v}_A = v_A\vec{\jmath}\qquad \vec{v}_B = v_B\vec{\jmath}

Para los tres casos siguientes:

  • vA = + vB
  • vA = 0
  • vA = − vB
  1. Indique justificadamente el tipo de movimiento instantáneo que realiza la esfera (traslación, rotación, helicoidal,…)
  2. Calcule la velocidad angular del sólido.
  3. Halle la velocidad angular de pivotamiento y la de rodadura de la esfera.
  4. Dé la ecuación del eje instantáneo de rotación y mínimo deslizamiento (o de rotación, en su caso).
  5. Calcule la velocidad lineal del centro C de la esfera y la del punto D situado en el extremo superior de la esfera.

Solución

7 Rodadura y pivotamiento de una esfera

Una esfera maciza de 2.5 cm de radio y 0.400 kg de masa rueda y pivota sin deslizar sobre una superficie horizontal. En un instante dado la velocidad angular de pivotamiento es de 1.80 rad/s en sentido antihorario respecto al eje OZ (tomando como origen el punto de contacto y como eje OZ el perpendicular al plano), mientras que la de rodadura es de 2.40 rad/s en la dirección del vector unitario

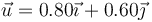
\vec{u}=0.80\vec{\imath}+0.60\vec{\jmath}

Para este instante, calcule:

  1. El vector velocidad angular y la ecuación del eje instantáneo de rotación.
  2. La velocidad y la rapidez del centro de la esfera.
  3. La distancia del centro de la esfera al eje instantáneo de rotación.
  4. La cantidad de movimiento, el momento cinético y la energía cinética de la esfera.

Dato: Momento de inercia de una esfera respecto a un eje que pasa por su centro I = (2 / 5)MR2.

Archivo:bola-sobre-plano.png

Solución

Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_cinem%C3%A1tica_del_s%C3%B3lido_r%C3%ADgido_(GIOI)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace