Problemas de cinemática del sólido rígido (GIOI)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Caso de campo de velocidades de un sólido== El campo de velocidades instantáneo de un sólido rígido tiene la expresión, en el sistema internacional <center><math>\vec{v}…') |
|||
| Línea 12: | Línea 12: | ||
[[Caso de campo de velocidades de un sólido|Solución]] | [[Caso de campo de velocidades de un sólido|Solución]] | ||
| + | |||
| + | ==Movimiento de un sólido conocido un eje== | ||
| + | Un sólido rígido se encuentra en rotación instantánea alrededor de un eje que pasa por el punto <math>A(1,0, - 1)</math> y lleva la dirección del vector <math>\vec{e}=2\vec{\imath}-2\vec{\jmath}-\vec{k}</math>, de tal forma que la velocidad del punto <math>B(0,2,1)</math> es <math>\vec{v}_B=-4\vec{\imath}-6\vec{\jmath}+c\vec{k}</math> | ||
| + | |||
| + | # Halle el valor de la constante <math>c</math>. | ||
| + | # Calcule la velocidad angular instantánea. | ||
| + | # Calcule la velocidad del punto <math>P(1,1,0)</math>. | ||
| + | |||
| + | Todas las cantidades están expresadas en las unidades del SI. | ||
| + | |||
| + | [[Movimiento de un sólido conocido un eje|Solución]] | ||
Revisión de 13:42 16 dic 2019
1 Caso de campo de velocidades de un sólido
El campo de velocidades instantáneo de un sólido rígido tiene la expresión, en el sistema internacional
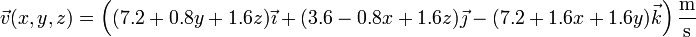
- Determine la velocidad angular,
, y la velocidad del origen de coordenadas, 
.
- Halle la velocidad del punto
.
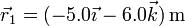- ¿Qué tipo de movimiento describe el sólido en este instante?
- Halle la ecuación del eje instantáneo de rotación y mínimo deslizamiento (o eje instantáneo de rotación, en su caso).
2 Movimiento de un sólido conocido un eje
Un sólido rígido se encuentra en rotación instantánea alrededor de un eje que pasa por el punto A(1,0, − 1) y lleva la dirección del vector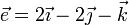 
, de tal forma que la velocidad del punto B(0,2,1) es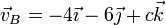 
- Halle el valor de la constante c.
- Calcule la velocidad angular instantánea.
- Calcule la velocidad del punto P(1,1,0).
Todas las cantidades están expresadas en las unidades del SI.
