Entrar Página Discusión Historial Go to the site toolbox

Test del primer parcial 2019-2020 (GIOI)

De Laplace

(Diferencias entre revisiones)
Línea 9: Línea 9:
;Solución:
;Solución:
La respuesta correcta es la '''<span style="color:red;">C<span>'''.
La respuesta correcta es la '''<span style="color:red;">C<span>'''.
-
+
 
 +
La partícula acelera con <math>a_0</math> durante un intervalo <math>T</math>. Durante ese tiempo la velocidad pasa de ser 0 a valer
 +
 
 +
<center><math>v(T)-v(0)=a_0T</math></center>
 +
 
 +
a partir de ahí, comienza a disminuir, con la mitad de la aceleración, pero el doble de tiempo, con lo que se reduce en
 +
 
 +
<center><math>v(3T)-v(T)=-\frac{a_0}{2}2T=-a_0T</math></center>
 +
 
 +
por lo que al final del intervalo completo
 +
 
 +
<center><math>v(3T)=a_0T-a_0T=0\,</math></center>
 +
 
 +
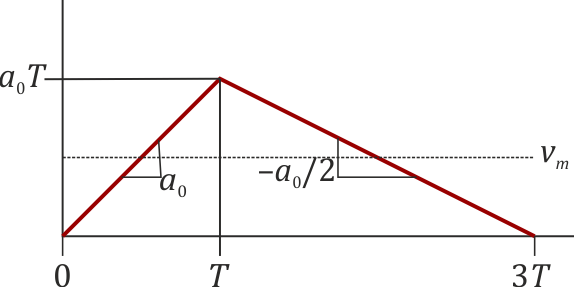
Gráficamente, la velocidad seguirá una curva como la de la figura.
 +
 
 +
<center>[[Archivo:velocidad-a-tramos.png]]</center>
 +
 
===Pregunta 2===
===Pregunta 2===
¿Cuál es el desplazamiento de la partícula entre <math>t=0</math> y <math>t=3T</math>?
¿Cuál es el desplazamiento de la partícula entre <math>t=0</math> y <math>t=3T</math>?
Línea 18: Línea 34:
;Solución:
;Solución:
La respuesta correcta es la '''<span style="color:red;">B<span>'''.
La respuesta correcta es la '''<span style="color:red;">B<span>'''.
 +
 +
Podemos responder simplemente observando que la velocidad media en los dos tramos es <math>a_0 T/2</math> con lo que el desplzamiento total es
 +
 +
<center><math>\Delta x = v_m\,\Delta t = \frac{a_0T}{2}(3T)=\frac{3a_0T^2}{2}</math></center>
 +
 +
Alternativamente, en el primer tramo tenemos, por ser un MRUA
 +
 +
<center><math>\Delta x_1=\frac{1}{2} a T^2 </math></center>
 +
 +
y en el segundo
 +
 +
<center><math>\Delta x_2=v_1 (2T)+\frac{1}{2}(-\frac{a_0}{2})(2T)^2= 2a_0T^2 - a_0T^2 = a_0T^2</math></center>
 +
 +
y sumando los dos tramos tenemps el resultado anterior.
==Cambio en la velocidad==
==Cambio en la velocidad==

Revisión de 22:19 5 nov 2019

Contenido

1 Aceleración a trozos

Una partícula se mueve en un movimiento rectilíneo que parte del reposo en x = 0. Durante un intervalo T se mueve con aceleración constante a0. A partir de ahí se mueve con aceleración constante − a0 / 2 durante un intervalo 2T.

1.1 Pregunta 1

¿Cuánto vale la velocidad de la partícula en t = 3T?

  • A − a0T.
  • B a0T.
  • C 0.
  • D a0T / 2.
Solución

La respuesta correcta es la C.

La partícula acelera con a0 durante un intervalo T. Durante ese tiempo la velocidad pasa de ser 0 a valer

v(T) − v(0) = a0T

a partir de ahí, comienza a disminuir, con la mitad de la aceleración, pero el doble de tiempo, con lo que se reduce en

v(3T)-v(T)=-\frac{a_0}{2}2T=-a_0T

por lo que al final del intervalo completo

v(3T)=a_0T-a_0T=0\,

Gráficamente, la velocidad seguirá una curva como la de la figura.

Archivo:velocidad-a-tramos.png

1.2 Pregunta 2

¿Cuál es el desplazamiento de la partícula entre t = 0 y t = 3T?

  • A − 3a0T2 / 2.
  • B 3a0T2 / 2.
  • C 0.
  • D − a0T2.
Solución

La respuesta correcta es la B.

Podemos responder simplemente observando que la velocidad media en los dos tramos es a0T / 2 con lo que el desplzamiento total es

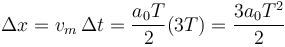
\Delta x = v_m\,\Delta t = \frac{a_0T}{2}(3T)=\frac{3a_0T^2}{2}

Alternativamente, en el primer tramo tenemos, por ser un MRUA

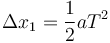
\Delta x_1=\frac{1}{2} a T^2

y en el segundo

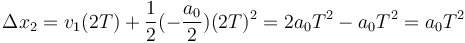
\Delta x_2=v_1 (2T)+\frac{1}{2}(-\frac{a_0}{2})(2T)^2= 2a_0T^2 - a_0T^2 = a_0T^2

y sumando los dos tramos tenemps el resultado anterior.

2 Cambio en la velocidad

En un movimiento en el plano OXY, la velocidad de una partícula en un instante dado es 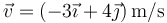\vec{v}=(-3\vec{\imath}+4\vec{\jmath})\,\mathrm{m}/\mathrm{s} y su aceleración en ese mismo instante es \vec{a}=(7\vec{\imath}-\vec{\jmath} )\,\mathrm{m}/\mathrm{s}^2.

2.1 Pregunta 1

En este instante la partícula está…

  • A ni frenando ni acelerando. Su rapidez es constante.
  • B frenando.
  • C acelerando.
  • D No hay información suficiente para saber si acelera o frena.
Solución

La respuesta correcta es la B.

2.2 Pregunta 2

En ese instante y, mirando desde el eje OZ positivo, la partícula…

  • A está desviándose hacia su izquierda.
  • B no se desvía, sino que avanza en línea recta.
  • C está desviándose hacia su derecha.
  • D No hay información suficiente para saber si cambia de dirección.
Solución

La respuesta correcta es la C.

3 Producto escalar y vectorial

Sean \vec{a} y \vec{b} dos vectores no nulos. Indique en qué caso se cumple la igualdad

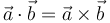
\vec{a}\cdot\vec{b}=\vec{a}\times\vec{b}
  • A Cuando \vec{a} y \vec{b} son paralelos.
  • B Cuando \vec{a} y \vec{b} son perpendiculares.
  • C Cuando \vec{a} y \vec{b} forman un ángulo de 45°.
  • D Nunca.
Solución

La respuesta correcta es la D.

4 Movimiento en polares

Una partícula describe un movimiento plano que, en polares, tiene la trayectoria ρ = kθ2, con k = cte. La trayectoria de este movimiento es

  • A Espiral.
  • B Circular.
  • C Helicoidal.
  • D Parabólica.
Solución

La respuesta correcta es la A.

5 Movimiento circular uniforme

¿Cuál de las siguientes afirmaciones es cierta para un movimiento circular uniforme alrededor del origen de coordenadas?

  • A La velocidad es perpendicular al vector de posición.
  • B La aceleración es nula.
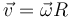  • C La velocidad es igual a \vec{v}=\vec{\omega}R.
  • D La aceleración es igual a |\vec{\omega} |^2 \vec{r}.
Solución

La respuesta correcta es la A.

6 Movimiento circular no uniforme

La figura ilustra la aceleración en varios instantes de un movimiento circular. ¿En cuál de ellos es máxima la rapidez?

  • A En P.
  • B En Q.
  • C En R.
  • D En S.
Solución

La respuesta correcta es la C.

Obtenido de "http://tesla.us.es/wiki/index.php/Test_del_primer_parcial_2019-2020_(GIOI)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace