Entrar Página Discusión Historial Go to the site toolbox

Otro caso particular de MAS (GIOI)

De Laplace

(Diferencias entre revisiones)
Antonio (Discusión | contribuciones)
(Página creada con '==Enunciado== Una partícula describe el movimiento armónico simple de ecuación horaria, en el SI, <center><math>x = 12\cos(2t)-5\,\mathrm{sen}(2t)</math></center> # ¿Cuanto…')
Edición más nueva →

Revisión de 13:52 3 oct 2019

Contenido

1 Enunciado

Una partícula describe el movimiento armónico simple de ecuación horaria, en el SI,

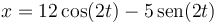
x = 12\cos(2t)-5\,\mathrm{sen}(2t)
  1. ¿Cuanto vale la amplitud de las oscilaciones?
  2. ¿Cuánto vale la velocidad inicial?
  3. ¿Cuánto vale la fase inicial?

2 Amplitud

La solución general del m.a.s. puede escribirse en las formas

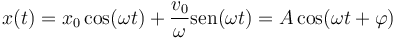
x(t)=x_0\cos(\omega t)+\frac{v_0}{\omega}\mathrm{sen}(\omega t)=A\cos(\omega t +\varphi)

La relación entre ambas se obtiene desarollando el coseno de una suma e identificando coeficientes

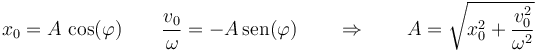
x_0=A\,\cos(\varphi)\qquad \frac{v_0}{\omega}=-A\,\mathrm{sen}(\varphi)\qquad\Rightarrow\qquad A=\sqrt{x_0^2+\frac{v_0^2}{\omega^2}}

En nuestro caso

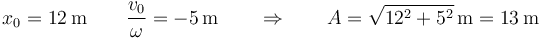
x_0=12\,\mathrm{m}\qquad \frac{v_0}{\omega}=-5\,\mathrm{m}\qquad\Rightarrow\qquad A=\sqrt{12^2+5^2}\,\mathrm{m}=13\,\mathrm{m}

3 Velocidad inicial

Por las relaciones anteriores

\frac{v_0}{\omega}=-5\,\mathrm{m}\qquad \omega = 2\,\frac{\mathrm{rad}}{\mathrm{s}}\qquad\Rightarrow\qquad v_0=-10\,\frac{\mathrm{m}}{\mathrm{s}}

4 fase inicial

Obtenido de "http://tesla.us.es/wiki/index.php/Otro_caso_particular_de_MAS_(GIOI)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace