Caso de movimiento parabólico (GIE)
De Laplace
(Diferencias entre revisiones)
Antonio (Discusión | contribuciones)
(Página creada con '==Enunciado== Una partícula se mueve con aceleración constante <math>\vec{a}_0=-4\vec{\imath}</math> (m/s²), siendo su posición inicial el origen de coordenadas y su velocid…')
Edición más nueva →
(Página creada con '==Enunciado== Una partícula se mueve con aceleración constante <math>\vec{a}_0=-4\vec{\imath}</math> (m/s²), siendo su posición inicial el origen de coordenadas y su velocid…')
Edición más nueva →
Revisión de 11:34 6 nov 2018
Enunciado
Una partícula se mueve con aceleración constante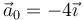 
(m/s²), siendo su posición inicial el origen de coordenadas y su velocidad inicial 
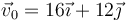(m/s).
- Halle su posición como función del tiempo.
- Determine el instante en que la rapidez o celeridad es mínima. Para este instante halle:
- La aceleración tangencial y la normal (escalares)
- Los vectores del triedro de Frenet
- El radio de curvatura
- El centro de curvatura
- Calcule en qué instante vuelve a pasar por el eje OY. Para este instante halle:
- La posición y la velocidad
- Los vectores del triedro de Frenet
- La aceleración tangencial y la normal (escalares)
