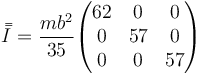Tensor de inercia de esfera hueca
De Laplace
(Página creada con '==Enunciado== Sea un sólido en forma de esfera maciza de radio 2b en la que se ha hecho una cavidad también esférica de radio b. La masa total del sólido es m. Determine el …') |
|||
| Línea 3: | Línea 3: | ||
<center>[[Archivo:esfera-hueca-descentrada.png|300px]]</center> | <center>[[Archivo:esfera-hueca-descentrada.png|300px]]</center> | ||
| + | |||
| + | ==Momentos de inercia== | ||
| + | Para el cálculo de los momentos de inercia y de los productos de inercia, aplicaremos el principio de superposición. Consideramos la esfera hueca como la superposición de dos esferas. | ||
| + | * Una esfera “1”, maciza de radio 2b y centro el origen, con masa <math>m_1</math>. | ||
| + | * Una esfera “2” maciza de radio b, centro <math>-b\vec{\imath}</math> y masa <math>m_2</math> (siendo <math>m_2</math> negativa). | ||
| + | |||
| + | Para que la superposición de las dos esferas nos de la esfera hueca que tenemos, la masa <math>m_2</math> debe anular la masa de la 1 contenida en el hueco. Por ser el radio la mitad, la masa contenida en esta parte es 1/8 de la total. Por tanto | ||
| + | |||
| + | <center><math>m_2+\frac{m_1}{8}=0 \qquad\Rightarrow\qquad m_2=-\frac{m_1}{8}</math></center> | ||
| + | |||
| + | Como por otro lado la masa total es m | ||
| + | |||
| + | <center><math>m_1+m_2=m\qquad\Rightarrow\qquad m_1-\frac{m_1}{8}=m\qquad\Rightarrow\qquad m_1=\frac{8}{7}m</math></center> | ||
| + | |||
| + | y | ||
| + | |||
| + | <center><math>m_2=-\frac{m}{7}</math></center> | ||
| + | ===Respecto al eje OX=== | ||
| + | El eje X pasa por los dos centros. Por tanto | ||
| + | |||
| + | <center><math>I_{xx}=\frac{2}{5}m_1R_1^2+\frac{2}{5}m_2R_2^2 = \frac{2}{5}\left(\frac{8m}{7}\right)(2b)^2+\frac{2}{5}\left(-\frac{m}{7}\right)b^2=\frac{62}{35}mb^2</math></center> | ||
| + | ===Respecto al eje OY=== | ||
| + | El eje OY pasa por el centro de la esfera grande, pero no por el de la pequeña. Para la primera tenemos | ||
| + | |||
| + | <center><math>I_{yy1}=\frac{2}{5}\left(\frac{8m}{7}\right)(2b)^2= \frac{64}{35}mb^2</math></center> | ||
| + | |||
| + | Para la segunda aplicamos el teorema de Steiner | ||
| + | |||
| + | <center><math>I_{yy2}=\frac{2}{5}m_2R_2^2+m_2 R_2^2= \frac{7}{5}m_2 R_2^2 = \frac{7}{5}\left(-\frac{m}{7}\right)b^2=-\frac{7mb^2}{35}</math></center> | ||
| + | |||
| + | lo que da en total | ||
| + | |||
| + | <center><math>I_{yy}=\frac{64-7}{35}mb^2=\frac{57}{35}mb^2</math></center> | ||
| + | |||
| + | ===Respecto al eje OZ=== | ||
| + | La posición del sólido respecto al eje OZ es idéntica a respecto al eje OY, por tanto | ||
| + | |||
| + | <center><math>I_{zz}=\frac{57}{35}mb^2</math></center> | ||
| + | ==Productos de inercia== | ||
| + | El plano XZ es un plano de simetría del sistema. Por tanto el eje OY es un eje principal del sólido. Esto implica que | ||
| + | |||
| + | <center><math>I_{xy}=0\qquad\qquad I_{yz}=0</math></center> | ||
| + | |||
| + | El plano XY también es de simetría. Por tanto OZ es principal y | ||
| + | |||
| + | <center><math>I_{xz}=0\qquad\qquad I_{xz}=0</math></center> | ||
| + | |||
| + | Es decir, los tres productos de inercia son nulos y el eje OX también es principal (como corresponde a un sólido de revolución) | ||
| + | |||
| + | ==Tensor de inercia== | ||
| + | Reuniendo los resultados anteriores queda la expresión matricial | ||
| + | |||
| + | <center><math>\bar{\bar{I}}=\frac{mb^2}{35}\begin{pmatrix}62 & 0 & 0 \\ 0 & 57 & 0 \\ 0 & 0 & 57\end{pmatrix}</math></center> | ||
| + | [[Categoría:Problemas de dinámica del sólido rígido (CMR)]] | ||
última version al 17:44 18 ago 2018
Contenido |
1 Enunciado
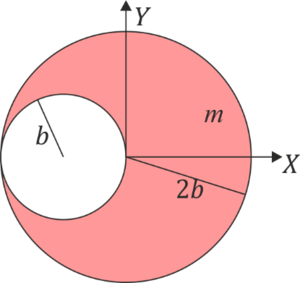
Sea un sólido en forma de esfera maciza de radio 2b en la que se ha hecho una cavidad también esférica de radio b. La masa total del sólido es m. Determine el tensor de inercia de este sólido respecto al sistema de referencia de la figura.
2 Momentos de inercia
Para el cálculo de los momentos de inercia y de los productos de inercia, aplicaremos el principio de superposición. Consideramos la esfera hueca como la superposición de dos esferas.
- Una esfera “1”, maciza de radio 2b y centro el origen, con masa m1.
- Una esfera “2” maciza de radio b, centro
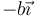y masa m2 (siendo m2 negativa).
Para que la superposición de las dos esferas nos de la esfera hueca que tenemos, la masa m2 debe anular la masa de la 1 contenida en el hueco. Por ser el radio la mitad, la masa contenida en esta parte es 1/8 de la total. Por tanto
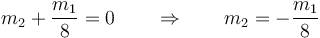
Como por otro lado la masa total es m
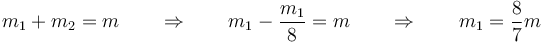
y
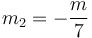
2.1 Respecto al eje OX
El eje X pasa por los dos centros. Por tanto
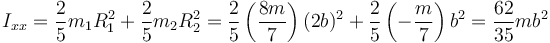
2.2 Respecto al eje OY
El eje OY pasa por el centro de la esfera grande, pero no por el de la pequeña. Para la primera tenemos
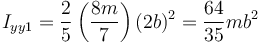
Para la segunda aplicamos el teorema de Steiner
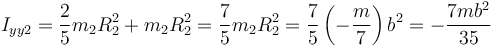
lo que da en total
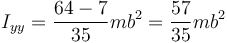
2.3 Respecto al eje OZ
La posición del sólido respecto al eje OZ es idéntica a respecto al eje OY, por tanto
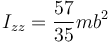
3 Productos de inercia
El plano XZ es un plano de simetría del sistema. Por tanto el eje OY es un eje principal del sólido. Esto implica que
El plano XY también es de simetría. Por tanto OZ es principal y
Es decir, los tres productos de inercia son nulos y el eje OX también es principal (como corresponde a un sólido de revolución)
4 Tensor de inercia
Reuniendo los resultados anteriores queda la expresión matricial
