Primera Convocatoria Ordinaria 2017/18 (G.I.C.)
De Laplace
(Diferencias entre revisiones)
(→Vuelco en plano inclinado) |
(→Armónicos en una cuerda tensa) |
||
| Línea 20: | Línea 20: | ||
Una cuerda de longitud <math>L=35.0\,\mathrm{m}</math> tiene una densidad de masa lineal | Una cuerda de longitud <math>L=35.0\,\mathrm{m}</math> tiene una densidad de masa lineal | ||
<math>\mu = 0.0850\,\mathrm{g/cm}</math> y soporta una tensión <math>F_T=18.0\,\mathrm{N}</math>. | <math>\mu = 0.0850\,\mathrm{g/cm}</math> y soporta una tensión <math>F_T=18.0\,\mathrm{N}</math>. | ||
| + | Se excita un onda estacionaria en la cuerda. | ||
Calcula las frecuencias de los dos primeros armónicos cuando | Calcula las frecuencias de los dos primeros armónicos cuando | ||
#los dos extremos están fijos. | #los dos extremos están fijos. | ||
#un extremo está fijo y el otro está libre. | #un extremo está fijo y el otro está libre. | ||
Revisión de 16:17 3 abr 2018
1 Vuelco en plano inclinado
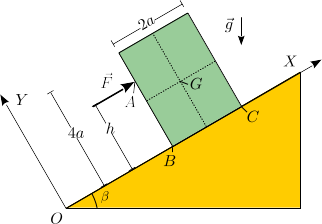
Un bloque rectangular, de masa m y lados 2a y 4a, descansa sobre
un plano inclinado un ángulo β respecto de la horizontal. Se aplica
sobre el punto A del bloque una fuerza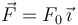 
, con F0 > 0. La fuerza es horizontal al plano inclinado y el punto A está a una
distancia h del plano. Consideramos en primera instancia que el contacto
entre el bloque y el plano es liso. El ángulo β cumple
- Dibuja el diagrama de cuerpo libre del bloque.
- Encuentra el valor de F0 para que haya equilibrio. Encuentra las expresiones de las fuerzas en esta situación.
- Con las fuerzas obtenidas en el apartado anterior, encuentra las condiciones que debe cumplir h para que el bloque no vuelque hacia la izquierda ni la derecha.
- Considera ahora que hay rozamiento entre el bloque y el plano inclinado, con coeficiente de rozamiento estático μ. Supongamos que F0 = mg. Determina las condiciones que deben cumplir μ y h para que haya equilibrio frente a deslizamiento y vuelco.
2 Armónicos en una cuerda tensa
Una cuerda de longitud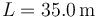 
tiene una densidad de masa lineal
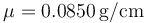y soporta una tensión 
.
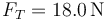Se excita un onda estacionaria en la cuerda.
Calcula las frecuencias de los dos primeros armónicos cuando
- los dos extremos están fijos.
- un extremo está fijo y el otro está libre.
