Dos discos en varilla giratoria
De Laplace
(Página creada con '==Enunciado== Categoría:Problemas de dinámica del sólido rígido (CMR)') |
|||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
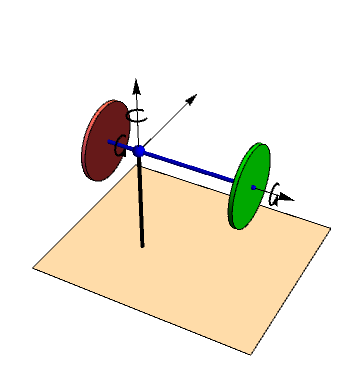
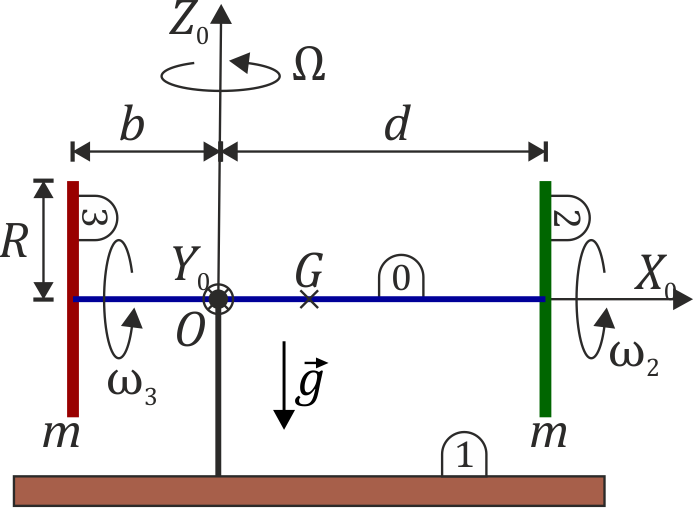
| + | Se tiene un sistema formado por dos discos idénticos, de masa <math>m</math> y radio <math>R</math> (sólidos “2” y “3”). Los discos está montados sobre un eje común (sólido “0”), que es una varilla ideal de masa despreciable. La unión de los discos a la varilla es mediante rodamientos que permiten un giro libre alrededor del eje. La varilla, a su vez está articulada en una rótula a un eje vertical. El punto de articulación, ''O'', no es el centro de la varilla, ''G'', sino que está a una distancia <math>d</math> del disco 2 y a una distancia <math>b</math> del disco 3. | ||
| + | El sistema está sometido a la acción del peso y la posible fuerza de reacción en O. | ||
| + | Tomamos un sistema de ejes rotatorio <math>OX_0Y_0Z_0</math> en el que el eje <math>OZ_0</math> es el vertical y el <math>OX_0</math> el que pasa por O y los centros de los dos discos. Todas las cantidades deben referirse a la base <math>\left\{\vec{\imath}_0,\vec{\jmath}_0,\vec{k}_0 \right\}</math>. | ||
| + | Supongamos que los discos giran respecto a su eje común, <math>OX_0</math>, con velocidades angulares constantes <math>\omega_2 \vec{\imath}_0</math> y <math>\omega_3 \vec{\imath}_0</math>, respectivamente, mientras la varilla gira respecto al eje vertical OZ_0 con velocidad angular constante <math>\Omega\vec{k}_0</math>. Para un instante dado: | ||
| + | # Determine las velocidades angulares de los dos discos respecto a un sistema fijo “1”, <math>\vec{\omega}_{21}</math> y <math>\vec{\omega}_{31}</math>. | ||
| + | # Para cada disco determine su tensor de inercia respecto al sistema <math>OX_0Y_0Z_0</math>. | ||
| + | # Calcule la cantidad de movimiento del sistema. | ||
| + | # Halle el momento cinético respecto al punto O de cada disco y el total, suma de los dos, | ||
| + | # Halle la energía cinética de cada disco y la total, suma de las dos. | ||
| + | # Determine la relación que debe haber entre <math>\omega_2</math>, <math>\omega_3</math> y <math>\Omega</math> en función de las masas, de g y de las dimensiones del sistema para que el sistema se mantenga girando uniformemente sin que sea preciso aplicar ningún par en O, de forma que el único momento sea el debido al peso. | ||
| + | # Halle la fuerza de reacción en O. | ||
| + | |||
| + | <center>[[Archivo:dos-discos-varilla-3D.png]]{{qquad}}{{qquad}}[[Archivo:dos-discos-varilla-esquema.png]]</center> | ||
[[Categoría:Problemas de dinámica del sólido rígido (CMR)]] | [[Categoría:Problemas de dinámica del sólido rígido (CMR)]] | ||
Revisión de 10:18 16 feb 2018
Enunciado
Se tiene un sistema formado por dos discos idénticos, de masa m y radio R (sólidos “2” y “3”). Los discos está montados sobre un eje común (sólido “0”), que es una varilla ideal de masa despreciable. La unión de los discos a la varilla es mediante rodamientos que permiten un giro libre alrededor del eje. La varilla, a su vez está articulada en una rótula a un eje vertical. El punto de articulación, O, no es el centro de la varilla, G, sino que está a una distancia d del disco 2 y a una distancia b del disco 3.
El sistema está sometido a la acción del peso y la posible fuerza de reacción en O.
Tomamos un sistema de ejes rotatorio OX0Y0Z0 en el que el eje OZ0 es el vertical y el OX0 el que pasa por O y los centros de los dos discos. Todas las cantidades deben referirse a la base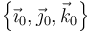 
.
Supongamos que los discos giran respecto a su eje común, OX0, con velocidades angulares constantes 
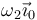y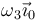 
, respectivamente, mientras la varilla gira respecto al eje vertical OZ_0 con velocidad angular constante 
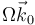. Para un instante dado:
- Determine las velocidades angulares de los dos discos respecto a un sistema fijo “1”,
y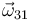 
.
- Para cada disco determine su tensor de inercia respecto al sistema OX0Y0Z0.
- Calcule la cantidad de movimiento del sistema.
- Halle el momento cinético respecto al punto O de cada disco y el total, suma de los dos,
- Halle la energía cinética de cada disco y la total, suma de las dos.
- Determine la relación que debe haber entre ω2, ω3 y Ω en función de las masas, de g y de las dimensiones del sistema para que el sistema se mantenga girando uniformemente sin que sea preciso aplicar ningún par en O, de forma que el único momento sea el debido al peso.
- Halle la fuerza de reacción en O.
