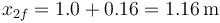Entrar Página Discusión Historial Go to the site toolbox

Colisión con rozamiento

De Laplace

(Diferencias entre revisiones)
Línea 1: Línea 1:
==Enunciado==
==Enunciado==
-
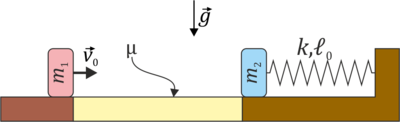
Sobre una superficie horizontal se encuentran dos masas. La masa <math>m_1=1.0\,\mathrm{kg}</math> se encuentra inicialmente en <math>x_{10}=0\,\mathrm{m}</math> y la masa <math>m_2=4.0\,\mathrm{kg}</math> en <math>x_{20}=1.0\,\mathrm{m}</math>. La masa 2 está unida a un resorte de constante <math>k=400\,\mathrm{N}/\mathrm{m}</math> y longitud en reposo <math>\ell_0=0.50\,\mathrm{m}</math>, estando inicialmente en la posición de equilibrio. El tramo de 1m entre la masa 1 y la 2 es una superficie rugosa, en la que la constante de rozamiento vale μ&thinsp;=&thinsp;0.45. El resto de la superficie está pulido.
+
Sobre una superficie horizontal se encuentran dos masas. La masa <math>m_1=1.0\,\mathrm{kg}</math> se encuentra inicialmente en <math>x_{10}=0\,\mathrm{m}</math> y la masa <math>m_2=4.0\,\mathrm{kg}</math> en <math>x_{20}=1.0\,\mathrm{m}</math>. La masa 2 está unida a un resorte de constante <math>k=400\,\mathrm{N}/\mathrm{m}</math> y longitud en reposo <math>\ell_0=0.50\,\mathrm{m}</math>, estando inicialmente en la posición de equilibrio. El tramo de 1&thinsp;m entre la masa 1 y la 2 es una superficie rugosa, en la que la constante de rozamiento vale μ&thinsp;=&thinsp;0.45. El resto de la superficie está pulido.
-
Estando las dos masas en reposo se le aplica una percusión a la masa 1 de forma que esta adquiere una velocidad inicial v_0=5\,m/s
+
Estando las dos masas en reposo se le aplica una percusión a la masa 1 de forma que esta adquiere una velocidad inicial <math>v_0=5\,\mathrm{m}/\mathrm{s}</math>
   
   
<center>[[Archivo:dos-masas-muelle-rozamiento.png|400px]]</center>
<center>[[Archivo:dos-masas-muelle-rozamiento.png|400px]]</center>
-
# Determine la velocidad de m_1 justo antes de impactar con la masa 2.
+
# Determine la velocidad de <math>m_1</math> justo antes de impactar con la masa 2.
# Calcule las velocidades de ambas masas justo tras el impacto. Suponga que la colisión es perfectamente elástica.
# Calcule las velocidades de ambas masas justo tras el impacto. Suponga que la colisión es perfectamente elástica.
# Halle la posición <math>x_{1f}</math> en la que se detiene la masa 1, si llega a hacerlo. Si no se detiene, halle la velocidad con la que llega a su posición inicial.
# Halle la posición <math>x_{1f}</math> en la que se detiene la masa 1, si llega a hacerlo. Si no se detiene, halle la velocidad con la que llega a su posición inicial.
# Halle la posición <math>x_{2f}</math> en la que se detiene m_2 por primera vez.
# Halle la posición <math>x_{2f}</math> en la que se detiene m_2 por primera vez.
Tómese <math>g=10\,\mathrm{m}/\mathrm{s}^2</math>.
Tómese <math>g=10\,\mathrm{m}/\mathrm{s}^2</math>.
 +
==Velocidad antes del impacto==
 +
Por el teorema trabajo-energía cinética
 +
 +
<center><math>\Delta K = W\qquad\Rightarrow\qquad \frac{1}{2}m_1v_{1i}^2-\frac{1}{2}m_1v_0^2 = -(\mu m_1g )\Delta x</math></center>
 +
 +
y da, para la velocidad de impacto
 +
 +
<center><math>v_{1i}=\sqrt{v_0^2-2\mu g\,\Delta x} = \sqrt{25-2\times 0.45\times 10\times 1}= 4\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
==Velocidades tras el impacto==
 +
Por la conservación de la cantidad de movimiento
 +
 +
<center><math>m_1 v_{1i}+m_2 v_{2i}=m_1 v_{1f} + m_2v_{2f}\qquad\Rightarrow\qquad v_{1f}+4v_{2f}=4</math></center>
 +
 +
Por ser una colisión elástica
 +
 +
<center><math>1 = \frac{v_{2f}-v_{1f}}{v_{1i}-v_{2i}}\qquad\Rightarrow\qquad v_{2f}-v_{1i}=4</math></center>
 +
 +
lo que da
 +
 +
<center><math>v_{1f}=-2.4\,\frac{\mathrm{m}}{\mathrm{s}}\qquad\qquad v_{1f}=1.6\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
==Detención de la masa 1==
 +
Aplicando el teorema trabajo-energía cinética
 +
 +
<center><math>0-\frac{1}{2}m_{1}v_{1f}^2=-\mu m_1 g \,\Delta x \qquad\Rightarrow\qquad \Delta x = \frac{v_{1f}^2}{2\mu g}=\frac{2.4^2}{2\times 0.45\times 10}=0.64\,\mathrm{m}</math></center>
 +
 +
Respecto a la posición inicial
 +
 +
<center><math>x_f=1.0-0.64 = 0.36\,\mathrm{m}</math></center>
 +
==Compresión del resorte==
 +
Por conservación de la energía mecánica
 +
 +
<center><math>\frac{1}{2}m_2 v_{2f}^2 + 0 = 0 + \frac{1}{2}k A^2 \qquad\Rightarrow\qquad A= \sqrt{\frac{m_2}{k}}\v_{2f}=\sqrt{\frac{4}{400}}1.6=0.16\,\mathrm{m}</math></center>
 +
 +
Respecto del origen de coordenadas
 +
 +
<center><math>x_{2f}=1.0+0.16 = 1.16\,\mathrm{m}</math></center>

Revisión de 23:50 31 ene 2018

Contenido

1 Enunciado

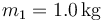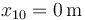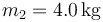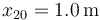Sobre una superficie horizontal se encuentran dos masas. La masa m_1=1.0\,\mathrm{kg} se encuentra inicialmente en x_{10}=0\,\mathrm{m} y la masa m_2=4.0\,\mathrm{kg} en x_{20}=1.0\,\mathrm{m}. La masa 2 está unida a un resorte de constante 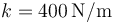k=400\,\mathrm{N}/\mathrm{m} y longitud en reposo 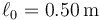\ell_0=0.50\,\mathrm{m}, estando inicialmente en la posición de equilibrio. El tramo de 1 m entre la masa 1 y la 2 es una superficie rugosa, en la que la constante de rozamiento vale μ = 0.45. El resto de la superficie está pulido.

Estando las dos masas en reposo se le aplica una percusión a la masa 1 de forma que esta adquiere una velocidad inicial 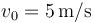v_0=5\,\mathrm{m}/\mathrm{s}

  1. Determine la velocidad de m1 justo antes de impactar con la masa 2.
  2. Calcule las velocidades de ambas masas justo tras el impacto. Suponga que la colisión es perfectamente elástica.
  3. Halle la posición x1f en la que se detiene la masa 1, si llega a hacerlo. Si no se detiene, halle la velocidad con la que llega a su posición inicial.
  4. Halle la posición x2f en la que se detiene m_2 por primera vez.

Tómese 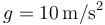g=10\,\mathrm{m}/\mathrm{s}^2.

2 Velocidad antes del impacto

Por el teorema trabajo-energía cinética

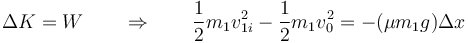
\Delta K = W\qquad\Rightarrow\qquad \frac{1}{2}m_1v_{1i}^2-\frac{1}{2}m_1v_0^2 = -(\mu m_1g )\Delta x

y da, para la velocidad de impacto

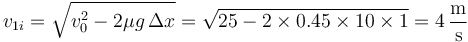
v_{1i}=\sqrt{v_0^2-2\mu g\,\Delta x} = \sqrt{25-2\times 0.45\times 10\times 1}= 4\,\frac{\mathrm{m}}{\mathrm{s}}

3 Velocidades tras el impacto

Por la conservación de la cantidad de movimiento

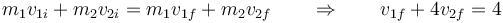
m_1 v_{1i}+m_2 v_{2i}=m_1 v_{1f} + m_2v_{2f}\qquad\Rightarrow\qquad v_{1f}+4v_{2f}=4

Por ser una colisión elástica

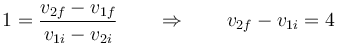
1 = \frac{v_{2f}-v_{1f}}{v_{1i}-v_{2i}}\qquad\Rightarrow\qquad v_{2f}-v_{1i}=4

lo que da

v_{1f}=-2.4\,\frac{\mathrm{m}}{\mathrm{s}}\qquad\qquad v_{1f}=1.6\,\frac{\mathrm{m}}{\mathrm{s}}

4 Detención de la masa 1

Aplicando el teorema trabajo-energía cinética

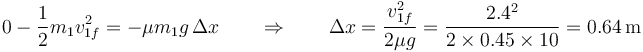
0-\frac{1}{2}m_{1}v_{1f}^2=-\mu m_1 g \,\Delta x \qquad\Rightarrow\qquad \Delta x = \frac{v_{1f}^2}{2\mu g}=\frac{2.4^2}{2\times 0.45\times 10}=0.64\,\mathrm{m}

Respecto a la posición inicial

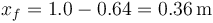
x_f=1.0-0.64 = 0.36\,\mathrm{m}

5 Compresión del resorte

Por conservación de la energía mecánica

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \frac{1}{2}m_2 v_{2f}^2 + 0 = 0 + \frac{1}{2}k A^2 \qquad\Rightarrow\qquad A= \sqrt{\frac{m_2}{k}}\v_{2f}=\sqrt{\frac{4}{400}}1.6=0.16\,\mathrm{m}

Respecto del origen de coordenadas

x_{2f}=1.0+0.16 = 1.16\,\mathrm{m}
Obtenido de "http://tesla.us.es/wiki/index.php/Colisi%C3%B3n_con_rozamiento"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace