Problemas de mecánica analítica (CMR)
De Laplace
(→Dos barras articuladas) |
(→Péndulo compuesto) |
||
| Línea 1: | Línea 1: | ||
| + | ==[[Estudio analítico de dos masas unidas por un muelle]]== | ||
| + | Como en el problema “[[Dos masas unidas por un muelle]]” tenemos dos masas <math>m_1</math> y <math>m_2</math> se mueven a lo largo del eje OX unidas por un resorte de constante <math>k</math> y longitud natura <math>\ell_0</math>. Inicialmente las dos masas se encuentran en reposo en <math>x_{10}=0</math> y <math>x_{20}=\ell_0</math>. Entonces se le comunica a la masa <math>m_1</math> una velocidad <math>v_0</math> en el sentido positivo del eje. | ||
| + | <center>[[Archivo:Dos-masas-muelle-horizontal.png|400px]]</center> | ||
| + | # Determine la lagrangiana del sistema en función de las posiciones de las dos partículas. | ||
| + | # Obtenga las ecuaciones de movimiento para <math>x_1</math> y <math>x_2</math> | ||
| + | Realice el cambio de variables a las coordenadas generalizadas <math>x_G=(m_1 x_1+m_2 x_2 )/(m_1+m_2 )</math>, <math>x=x_2-x_1-\ell_0</math>. | ||
| + | <ol start="3"> | ||
| + | <li>¿Cómo queda la lagrangiana en función de estas coordenadas?</li> | ||
| + | <li>Obtenga las ecuaciones de movimiento para x_G y x.</li> | ||
| + | <li>Determine dos constantes de movimiento para este sistema.</li> | ||
| + | </ol> | ||
| + | |||
==[[Péndulo compuesto. Análisis por mecánica analítica (CMR)|Péndulo compuesto]]== | ==[[Péndulo compuesto. Análisis por mecánica analítica (CMR)|Péndulo compuesto]]== | ||
Para el sistema del problema “[[Péndulo compuesto (CMR)|Péndulo compuesto]]” analice el problema general mediante las técnicas de mecánica analítica. Se tiene una barra homogénea de longitud b y masa m, articulada mediante una rótula en un extremo O y sometida a la acción de la gravedad. La barra puede tanto variar su ángulo θ con la vertical como el ángulo ϕ alrededor de OZ. | Para el sistema del problema “[[Péndulo compuesto (CMR)|Péndulo compuesto]]” analice el problema general mediante las técnicas de mecánica analítica. Se tiene una barra homogénea de longitud b y masa m, articulada mediante una rótula en un extremo O y sometida a la acción de la gravedad. La barra puede tanto variar su ángulo θ con la vertical como el ángulo ϕ alrededor de OZ. | ||
Revisión de 10:35 20 ene 2018
1 Estudio analítico de dos masas unidas por un muelle
Como en el problema “Dos masas unidas por un muelle” tenemos dos masas m1 y m2 se mueven a lo largo del eje OX unidas por un resorte de constante k y longitud natura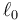 
. Inicialmente las dos masas se encuentran en reposo en x10 = 0 y 
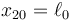. Entonces se le comunica a la masa m1 una velocidad v0 en el sentido positivo del eje.
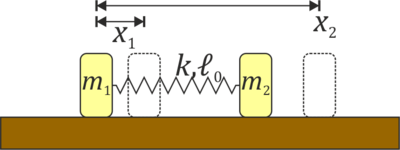
- Determine la lagrangiana del sistema en función de las posiciones de las dos partículas.
- Obtenga las ecuaciones de movimiento para x1 y x2
Realice el cambio de variables a las coordenadas generalizadas xG = (m1x1 + m2x2) / (m1 + m2), 
.
- ¿Cómo queda la lagrangiana en función de estas coordenadas?
- Obtenga las ecuaciones de movimiento para x_G y x.
- Determine dos constantes de movimiento para este sistema.
2 Péndulo compuesto
Para el sistema del problema “Péndulo compuesto” analice el problema general mediante las técnicas de mecánica analítica. Se tiene una barra homogénea de longitud b y masa m, articulada mediante una rótula en un extremo O y sometida a la acción de la gravedad. La barra puede tanto variar su ángulo θ con la vertical como el ángulo ϕ alrededor de OZ.
Para este sistema
- Calcule la lagrangiana del sistema.
- Halle las ecuaciones de movimiento para los dos ángulos de giro, θ y ϕ
- Obtenga dos constantes de movimiento no triviales.
- Con ayuda de las constantes de movimiento, halle una ecuación que incluya solamente a θ
- Calcule el valor que debe tener la velocidad angular
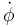si se desea que la barra mantenga una inclinación constante respecto a la vertical.
3 Dos barras articuladas
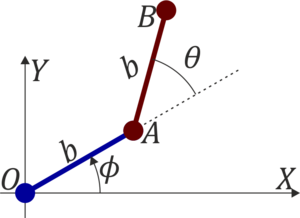
Un sistema está formado por dos varillas homogéneas, ambas de masa m y longitud b, situadas sobre un plano horizontal (“sólido 1”). La varilla “2” está articulada por su extremo O a un punto fijo del plano, mientras que por su extremo A está articulada a la varilla “3”.
- Escriba la lagrangiana del sistema, empleando como coordenadas generalizadas los ángulos que ambas varillas forman con el eje OX.
- Obtenga las ecuaciones de movimiento para estos dos ángulos.
- ¿Es cíclica alguna de estas coordenadas?
Si en lugar de esas coordenadas se usan el ángulo ϕ que la varilla OA forma con OX y el ángulo θ que AB forma con la prolongación de OA
- ¿Cómo queda la lagrangiana?
- ¿Y las ecuaciones de movimiento para estos ángulos?
- ¿Es cíclica alguna de estas coordenadas?
- Determine dos constantes de movimiento para este sistema.
- Con ayuda de estas constantes, reduzca el problema a una única ecuación de movimiento para el ángulo θ.
Suponga ahora que la varilla 2 es forzada a girar con velocidad angular constante Ω en torno a O.
- Escriba la lagrangiana para este sistema en función del ángulo θ.
- Obtenga la ecuación de movimiento para θ. ¿Es la misma que en el apartado (8)?
- ¿Se conserva la energía en este sistema? ¿Hay alguna otra constante de movimiento?
