Medio polarizado entre dos placas
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Enunciado== Una corteza esférica de radio interior <math>a</math> y exterior <math>b</math> está hecha de dieléctrico polarizado según la ley <center><math>\mathbf{P} = \frac{...) |
(→Solución) |
||
| Línea 11: | Línea 11: | ||
==Solución== | ==Solución== | ||
| - | + | ===Cargas de polarización=== | |
| + | ====De volumen==== | ||
| + | ====De superficie==== | ||
| + | ====Carga total==== | ||
| + | ===Campos=== | ||
| + | ====Vector desplazamiento==== | ||
| + | ====Campo eléctrico==== | ||
| + | ===Potencial eléctrico=== | ||
[[Categoría:Problemas de materiales dieléctricos]] | [[Categoría:Problemas de materiales dieléctricos]] | ||
Revisión de 13:59 13 feb 2009
Contenido |
1 Enunciado
Una corteza esférica de radio interior a y exterior b está hecha de dieléctrico polarizado según la ley
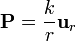
No hay más cargas en el sistema
- Calcule las densidades de carga de polarización en el sistema. ¿Cuánto vale la carga total de polarización?
- Halle los campos
 y
y  en todo el espacio.
en todo el espacio.
- Determine el valor del potencial eléctrico en todo el espacio.





