Partícula en anilla giratoria
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
|||
| Línea 6: | Línea 6: | ||
<center>[[Archivo:anillla-aro-rotatorio.png|300px]]</center> | <center>[[Archivo:anillla-aro-rotatorio.png|300px]]</center> | ||
| + | |||
| + | ==Ecuación del vínculo== | ||
| + | La partícula está obligada a moverse sobre una línea, la cual la podemos considerar como una intersección de dos superficies: | ||
| + | |||
| + | * Una esfera de radio b | ||
| + | |||
| + | <center><math>x^2+y^2+z^2=b^2\,</math></center> | ||
| + | |||
| + | :o, en cilíndricas, | ||
| + | |||
| + | <center><math>\rho^2+z^2 = b^2\,</math></center> | ||
| + | |||
| + | :o, en esféricas, | ||
| + | |||
| + | <center><math>r=b\,</math></center> | ||
| + | * Un plano giratorio. Este plano fija la coordenada θ de cilíndricas, en | ||
| + | |||
| + | <center><math>\theta=\Omega t\,</math></center> | ||
| + | |||
| + | :(que sería <math>\varphi=\Omega t</math> en esféricas). En cartesianas, sería | ||
| + | |||
| + | <center><math>\frac{y}{x}=\mathrm{tg}(\Omega t)\qquad\Rightarrow\qquad -x\,\mathrm{sen}(\Omega t)+y\cos(\Omega t)=0</math></center> | ||
| + | |||
| + | Este vínculo es liso, bilateral, reónomo (pues depende del tiempo) y geométrico. Al ser geométrico, es también holónomo. | ||
| + | ==Puntos de equilibrio== | ||
| + | ==Equilibrio con rozamiento== | ||
Revisión de 10:27 2 dic 2017
Contenido |
1 Enunciado
Una pequeña anilla de masa m está ensartada sin rozamiento en un aro circular de masa M y radio b situado verticalmente que puede girar en torno a un diámetro vertical. Suponga que este aro se hace girar con velocidad angular constante Ω alrededor de este diámetro.
- Escriba la ecuación del vínculo sobre la partícula. ¿De qué tipo es?
- Determine la posición de los posibles puntos de equilibrio en la vertical, así como la estabilidad de éstos, en función del valor de Ω.
- Suponga ahora que entre la anilla y el aro existe un coeficiente de rozamiento seco μ, ¿cómo queda en ese caso la ecuación de movimiento para la anilla? Para un valor de Ω dado, ¿cuál es en ese caso el rango de posiciones verticales de equilibrio?
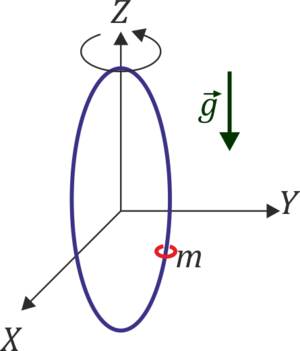
2 Ecuación del vínculo
La partícula está obligada a moverse sobre una línea, la cual la podemos considerar como una intersección de dos superficies:
- Una esfera de radio b

- o, en cilíndricas,
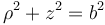
- o, en esféricas,

- Un plano giratorio. Este plano fija la coordenada θ de cilíndricas, en
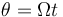
- (que sería
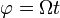 en esféricas). En cartesianas, sería
en esféricas). En cartesianas, sería
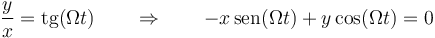
Este vínculo es liso, bilateral, reónomo (pues depende del tiempo) y geométrico. Al ser geométrico, es también holónomo.





