Partícula en anilla giratoria
De Laplace
Contenido |
1 Enunciado
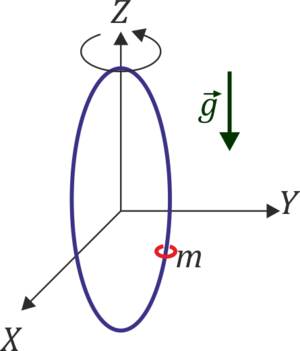
Una pequeña anilla de masa m está ensartada sin rozamiento en un aro circular de masa M y radio b situado verticalmente que puede girar en torno a un diámetro vertical. Suponga que este aro se hace girar con velocidad angular constante Ω alrededor de este diámetro.
- Escriba la ecuación del vínculo sobre la partícula. ¿De qué tipo es?
- Determine la posición de los posibles puntos de equilibrio en la vertical, así como la estabilidad de éstos, en función del valor de Ω.
- Suponga ahora que entre la anilla y el aro existe un coeficiente de rozamiento seco μ, ¿cómo queda en ese caso la ecuación de movimiento para la anilla? Para un valor de Ω dado, ¿cuál es en ese caso el rango de posiciones verticales de equilibrio?
2 Ecuación del vínculo
La partícula está obligada a moverse sobre una línea, la cual la podemos considerar como una intersección de dos superficies:
- Una esfera de radio b

- o, en cilíndricas,
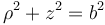
- o, en esféricas,

- Un plano giratorio. Este plano fija la coordenada θ de cilíndricas, en
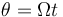
- (que sería
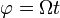 en esféricas). En cartesianas, sería
en esféricas). En cartesianas, sería
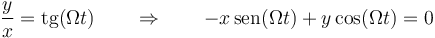
Este vínculo es liso, bilateral, reónomo (pues depende del tiempo) y geométrico. Al ser geométrico, es también holónomo.
3 Ecuaciones de movimiento
3.1 Coordenadas
Para describir el movimiento emplearemos la base de cilíndricas y parametrizamos la ecuación de la curva como
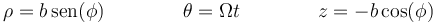
siendo φ el ángulo con la vertical descendente. En realidad, esto equivale a usar coordenadas esféricas, pero lo haremos así para aprovechar las fórmulas de coordenadas cilíndricas, más fáciles de recordar.
Empleando la abreviatura, que usaremos en lo sucesivo

estas coordenadas se escriben
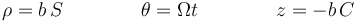
Las derivadas respecto al tiempo valen, por la regla de la cadena
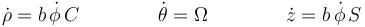
y las segundas derivadas

3.2 Velocidad y aceleración
3.2.1 Velocidad
Sustituímos en la expresión de la velocidad en cilíndricas

3.2.2 Aceleración
De la misma manera obtenemos la aceleración. Si separamos por componentes queda, para la componente cilíndrica radial
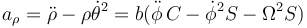
para la acimutal
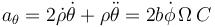
y para la vertical
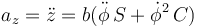
3.3 Fuerzas
En ausencia de rozamiento, la partícula está sometida a dos fuerzas: el peso y la reacción del aro.
A su vez, la reacción la podemos descomponer en dos partes, cada una correspondiente a una ecuación del vínculo. La primera impide que la partícula se mueva radialmente, por lo que tendrá una dirección radial respecto al centro del aro
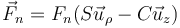
Se puede hallar esta dirección calculando el gradiente de la ecuación del vínculo y escribiendo un vector paralelo a este gradiente.
Para la segunda ecuación tenemos una fuerza acimutal que es la que obliga a la anilla a dar vueltas con el aro
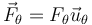
Las dos cantidades Fn y Fθ son también incógnitas que habrá que determinar.
3.4 Segunda ley de Newton
Sustituyendo la aceleración y las fuerzas en la segunda ley de Newton obtenemos las ecuaciones de movimiento siguientes. Para la componente cilíndrica radial
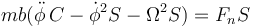
para la acimutal
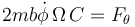
y para la vertical
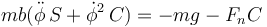
Si multiplicamos la primera por C y la tercera por S y sumamos eliminamos la fuerza normal
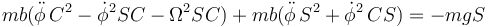
Simplificamos aquí y queda
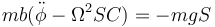
o, equivalentemente
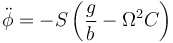
que es la ecuación de movimiento para la coordenada φ. Podemos comprobar que, en ausencia de rotación, se reduce a la ecuación del péndulo simple
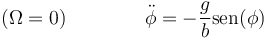
4 Puntos de equilibrio
===Posiciones de equilibrio===& Si el aro no girara, habría solo dos posiciones de equilibrio, una en el punto más bajo y otra en el punto más alto. La primera sería estable y la segunda inestable.
La rotación del aro introduce nuevas posiciones de equilibrio. Podemos visualizarlo imaginando la acción de una fuerza centrífuga que apunta hacia el exterior, posibilitando que la anilla se quede estacionaria a una cierta altura.
Hay que señalar que en ese caso, estas posiciones serían estacionarias respecto al aro, pero no respecto a un observador exterior, el cual vería la anilla dar vueltas alrededor del eje, como el resto del aro en que se halla ensartada.
Determinamos las posiciones de equilibrio a partir de la ecuación de movimiento. En el equilibrio la segunda derivada de φ debe ser nula, ya que si no la partícula saldría de la posición. Esto nos da la ecuación
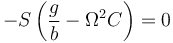
que ofrece las siguientes posibilidades:
- que se anule el primer factor
- con dos soluciones
-
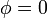 . El punto más bajo del aro.
. El punto más bajo del aro.
-
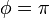 . El punto más alto.
. El punto más alto.
-
- Que se anule el segundo factor
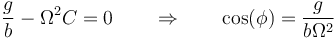
- Esta ecuación no siempre tiene solución real.
- Si
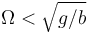 resultaría un coseno mayor que la unidad y por tanto no hay solución-
resultaría un coseno mayor que la unidad y por tanto no hay solución-
- Si
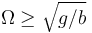 aparecen dos nuevas soluciones:
aparecen dos nuevas soluciones:
- Si
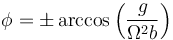
- Estas corresponden a posiciones simétricas alrededor del eje de rotación.
Hay que destacar que estas posiciones no son estacionarias. Cuando el aro gira, la anilla se mueve con él y por tanto su velocidad y su aceleración no son nulas.
4.1 Estabilidad del equilibrio
La estabilidad del equilibrio la podemos determinar a partir de la propia ecuación de movimiento o a partir de la energía.
4.1.1 A partir de la ecuación de movimiento
El procedimiento consiste en linealizar la ecuación de movimiento alrededor de la posición de equilibrio. Si resulta una ecuación de tipo del oscilador armónico
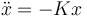
la posición de equilibrio es estable. Si por el contrario queda de la forma
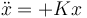
la posición es repulsiva y el equilibrio es inestable.
Analizamos los casos que nos han aparecido:
- Punto más bajo del aro
Cuando el ángulo φ es muy pequeño podemos hacer la aproximación

lo que nos permite aproximar la ecuación de movimiento por

que nos da dos posibilidades:
- Si
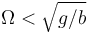 este punto de equilibrio es estable.
este punto de equilibrio es estable.
- Si
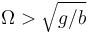 el punto es inestable.
el punto es inestable.
El caso de igualdad es lo que se conoce como una bifurcación, pasando de un estado al otro.
- Punto más alto del aro
Cuando el ángulo 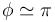 podemos hacer la sustitución
podemos hacer la sustitución

con lo que se cumple
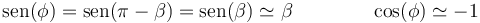
y
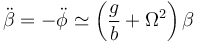
El coeficiente es siempre positivo, por lo que este punto es siempre inestable, como cabe esperar.
- Puntos laterales
- Suponiendo que Ω supera el valor crítico, tenemos los puntos definidos por la ecuación
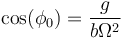
Si suponemos un ángulo próximo a este valor

queda
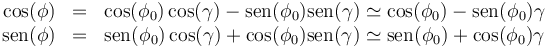
Llevamos esto a la ecuación de movimiento
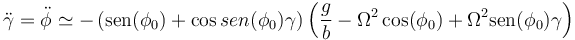
Ahora bien, por la ecuación que define a φ0 se cancelan términos y esta expresión se reduce a

El coeficiente es siempre negativo y por tanto los dos puntos simétricos son de equilibrio estable.
Resumiendo tenemos las siguientes posibilidades:
- Si
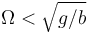 hay un punto estable en el punto más bajo del aro y uno inestable en el más alto.
hay un punto estable en el punto más bajo del aro y uno inestable en el más alto.
- Si
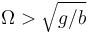 los dos anteriores son inestables y aparecen dos estables situados simétricamente.
los dos anteriores son inestables y aparecen dos estables situados simétricamente.
4.1.2 A partir de la energía
Parecería más simple hallr los puntos de equilibrio buscando los mínimos de la energía potencial. Sin embargo, ese procedimiento no se puede aplicar aquí porque este sistema no es conservativo.
En el caso de un vínculo reónomo, como este, las fuerzas de reacción vincular sí pueden realizar trabajo ya que empujan en la dirección de movimiento. En ese caso no se conserva la energía mecánica, sino que se cumple
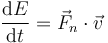
No obstante, puede encontrarse una magnitud similar a la energía mecánica que sí se conserva y una magnitud similar a la energía potencial cuyos extremos nos dan las posiciones de equilibrio.
La potencia que desarrolla la fuerza de reacción vale
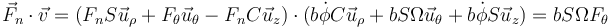
Vemos que es solo la componente acimutal la que desarrolla potencia.
De las ecuaciones de movimiento tenemos que

lo que nos da la potencia
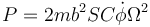
Ahora bien, esta cantidad es la derivada con respecto al tiempo de
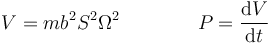
Por tanto la ley para la energía mecánica se convierte en
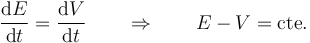
Esta energía efectiva que sí se conserva tiene la expresión
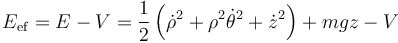
Sustituimos aquí las diferentes derivadas y queda
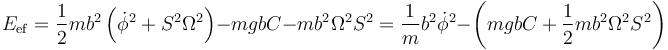
Esta expresión tiene la misma forma que la de una partícula en un movimiento circular sometida a la energía potencial efectiva
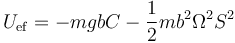
Son los extremos de esta función los que nos dan las posiciones de equilibrio
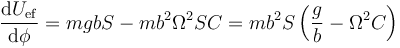
Vemos que llegamos a la misma ecuación para localizar los puntos de equilibrio. Derivamos de nuevo
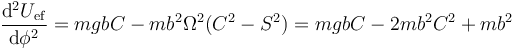
Entonces tenemos:
- En el punto más bajo, el coseno vale +1 y queda
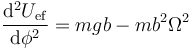
- que es positivo (estable) para valores pequeños de Ωy negativo (inestable) para valores grandes.
- En el punto más alto el coseno vale −1.
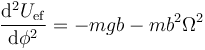
- que es siempre negativo y el punto es siempre inestable.
- En los puntos laterales el coseno cumple
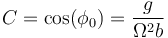
- y queda
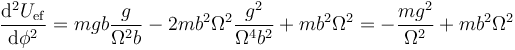
- Dado que en estos puntos Ω2 > (g / b), esta cantidad es siempre positiva y los puntos son estables.
También podemos analizar la estabilidad gráficamente trazando las curvas de Uef(φ) para distintos valores de Ω.
5 Equilibrio con rozamiento
En presencia de rozamiento, es necesario añadir una fuerza tangente al aro. Esta será de la forma

de manera que las ecuaciones de movimiento quedan: Para la componente cilíndrica radial
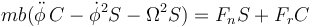
para la acimutal
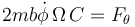
y para la vertical
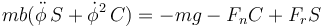
Si solo deseamos las posiciones de equilibrio, podemos hacer 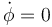 y
y 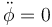 , lo que nos deja con la ecuación para la componente cilíndrica radial
, lo que nos deja con la ecuación para la componente cilíndrica radial
para la acimutal
y para la vertical
Combinando las ecuaciones podemos determinar las fuerzas de reacción
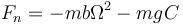
y de rozamiento
La fuerza de rozamiento seco debe cumplir

que para una sola componente se reduce a
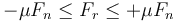
En nuestro caso
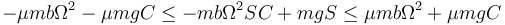
Los casos límite corresponden a la igualdad, resultando las ecuaciones para el valor mínimo

y para el máximo

Si alguna de estas dos ecuaciones produce un valor negativo, el valor mínimo se hace 0.





