Problemas de cinemática de la partícula (CMR)
De Laplace
(Diferencias entre revisiones)
Antonio (Discusión | contribuciones)
(Página creada con '==Cálculo de velocidad media== Una partícula describe un movimiento rectilíneo tal que su velocidad instantánea cumple la ley <center>…')
Edición más nueva →
(Página creada con '==Cálculo de velocidad media== Una partícula describe un movimiento rectilíneo tal que su velocidad instantánea cumple la ley <center>…')
Edición más nueva →
Revisión de 18:30 12 oct 2017
1 Cálculo de velocidad media
Una partícula describe un movimiento rectilíneo tal que su velocidad instantánea cumple la ley
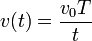
¿Cuánto vale la velocidad media entre 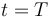 y
y 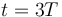 ?
?
2 Tiro parabólico sobre una pendiente
Se desea alcanzar un blanco que se encuentra sobre un plano inclinado un ángulo β, estando el blanco a una distancia D del punto de disparo.
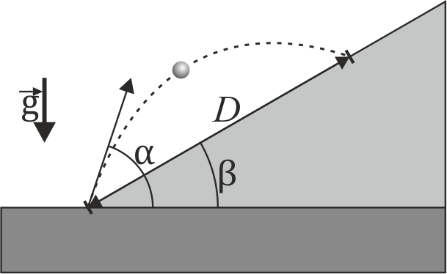
- ¿Cuál es la rapidez mínima que debe tener el proyectil para llegar al blanco? ¿Con qué ángulo sobre la horizontal debe dispararse en ese caso?
- Suponga que el plano tiene una pendiente del 75% y el proyectil se lanza con el ángulo que da el alcance máximo para llegar a D = 100 m. Para este caso, halle:
- La rapidez que tiene en el momento del impacto.
- La aceleración tangencial y normal (escalares) en el momento de impacto.
Tómese 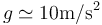 .
.
3 Análisis de ecuación horaria
Una partícula se mueve por el espacio de forma que su velocidad, en las unidades fundamentales del SI, viene dada por la ecuación horaria
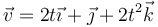
Inicialmente la partícula se encuentra en 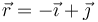 .
.
- Calcule la posición en función del tiempo y el desplazamiento entre
 y
y 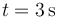 . ¿Cuánto vale la velocidad media en dicho intervalo?
. ¿Cuánto vale la velocidad media en dicho intervalo?
- Halle la rapidez en cada instante, así como la distancia que recorre la partícula en el mismo intervalo de tiempo. ¿Cuánto vale la rapidez media en este intervalo?
- Halle las componentes intrínsecas de la aceleración en
 , como escalares y como vectores.
, como escalares y como vectores.
- Halle el triedro de Frenet en
 .
.
- Calcule el radio de curvatura en
 así como el centro de curvatura en ese instante.
así como el centro de curvatura en ese instante.





