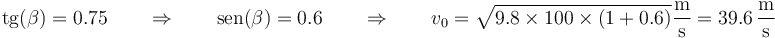Tiro parabólico sobre una pendiente

De Laplace

(Diferencias entre revisiones)

Revisión de 10:30 8 oct 2017

Contenido

1 Enunciado
2 Rapidez mínima
3 Caso particular
- 3.1 Rapidez de lanzamiento

1 Enunciado

Se desea alcanzar un blanco que se encuentra sobre un plano inclinado un ángulo β, estando el blanco a una distancia D del punto de disparo.

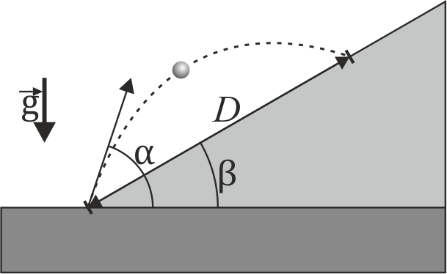
¿Cuál es la rapidez mínima que debe tener el proyectil para llegar al blanco? ¿Con qué ángulo sobre la horizontal debe dispararse en ese caso?
Suponga que el plano tiene una pendiente del 75% y el proyectil se lanza con el ángulo que da el alcance máximo para llegar a D = 100 m. Para este caso, halle:
1. La rapidez que tiene en el momento del impacto.
2. La aceleración tangencial y normal (escalares) en el momento de impacto.

Tómese 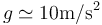$g\simeq 10\mathrm{m}/\mathrm{s}^2$ .

2 Rapidez mínima

La rápidez de lanzamiento mínima para llegar a un punto es aquella que tiene la distancia al punto como alcance máximo. Si no fuera así, siempre podría reducirse la rapidez de lanzamiento y llegar al mismo punto.

Para obtener esta rapidez hallaremos primero las condiciones para que impacte en un punto cualquiera, máximo o no, luego veremos en qué condiciones este alcance es máximo y a partir de ahí obtendremos la rapidez mínima.

2.1 Alcance general

En el movimiento del proyectil, se cumplen las ecuaciones horarias

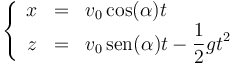
$\left\{\begin{array}{rcl} x & = & v_0\cos(\alpha)t \\ z & = & v_0\,\mathrm{sen}(\alpha)t-\displaystyle\frac{1}{2}gt^2\end{array}\right.$

Por otro lado, en el momento de impacto, el proyectil se encuentra sobre la pendiente, por lo que

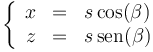
$\left\{\begin{array}{rcl} x & = & s\cos(\beta) \\ z & = & s\,\mathrm{sen}(\beta)\end{array}\right.$

Para hallar el punto de impacto, debemos resolver este sistema de dos ecuaciones con dos incógnitas ( $t$ y $s$ ), lo cual se puede hacer de diversas formas. Una vez que hayamos calculado el alcance, buscaremos su valor máximo con respecto al ángulo de lanzamiento.

Primero despejamos el tiempo de impacto

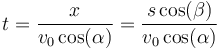
$t=\frac{x}{v_0\cos(\alpha)}=\frac{s\cos(\beta)}{v_0\cos(\alpha)}$

y a continuación sustituimos en la coordenada vertical

$s\,\mathrm{sen}(\beta)= z = \frac{s\,\mathrm{sen}(\alpha)\cos(\beta)}{\cos(\alpha)}-\frac{g\,\cos^2(\beta)s^2}{2v_0^2\cos^2(\alpha)}$

Dividiendo por s en cada miembro obtenemos una ecuación de primer grado

$\mathrm{sen}(\beta)=\frac{\mathrm{sen}(\alpha)\cos(\beta)}{\cos(\alpha)} - \frac{g\cos^2(\beta)}{2v_0^2\cos^2(\alpha)}s$

Despejamos de aquí el alcance

$s = \frac{2v_0^2\cos(\alpha)\left(\mathrm{sen}(\alpha)\cos(\beta)-\mathrm{sen}(\beta)\cos(\alpha)\right)}{g\cos^2(\beta)}$

Esta expresión se puede simplificar con ayuda de las relaciones trigonométricas y escribirse como

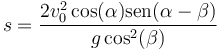
$s = \frac{2v_0^2\cos(\alpha)\mathrm{sen}(\alpha-\beta)}{g\cos^2(\beta)}$

A modo de comprobación, vemos que para un plano horizontal se obtiene el resultado conocido

$(\beta=0) \qquad s = \frac{2v_0^2\cos(\alpha)\mathrm{sen}(\alpha-0)}{g\cdot 1}=\frac{v_0^2\mathrm{sen}(2\alpha)}{g}$

2.2 Alcance máximo

Podemos hallar el alcance máximo sin necesidad de derivar e igualar a cero con ayuda de la relación trigonométrica

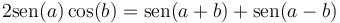
$2\mathrm{sen}(a)\cos(b)=\mathrm{sen}(a+b)+\mathrm{sen}(a-b)\,$

que en este caso da

$s = \frac{v_0^2\left(\mathrm{sen}(2\alpha-\beta)-\mathrm{sen}(\beta)\right)}{g\cos^2(\beta)}$

En esta expresión la única dependencia en $α$ está en el numerador. Por tanto, el máximo valor del alcance lo obtenemos cuando ese seno es igual a la unidad

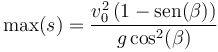
$\max(s)= \frac{v_0^2\left(1-\mathrm{sen}(\beta)\right)}{g\cos^2(\beta)}$

que se da para

$\mathrm{sen}(2\alpha-\beta)=1\qquad\Rightarrow\qquad 2\alpha-\beta = \frac{\pi}{2}\qquad\Rightarrow\qquad \alpha = \frac{\pi}{4}+\frac{\beta}{2}$

Podemos simplificar el máximo alcance haciendo uso de otra relación trigonométrica

cos 2 (β) = 1 - sen 2 (β) = (1 - sen(β))(1 + sen(β))

y queda

$\max(s)= \frac{v_0^2}{g\left(1+\mathrm{sen}(\beta)\right)}$

Comprobamos los casos límite conocidos

Para el plano horizontal $β = 0$ y resulta el ángulo de máximo alcance y el valor de éste

$\alpha = \frac{\pi}{4}+0=45^\circ \qquad\qquad \max(s) = \frac{v_0^2}{g}$

Para una pared vertical $β = π / 2$ y resulta

$\alpha = \frac{\pi}{4}+\frac{\pi}{4}=\frac{\pi}{2}=90^\circ \qquad\qquad \max(s) = \frac{v_0^2}{2g}$

que quiere decir que, lógicamente, debemos lanzar el proyectil en vertical y el alcance será la máxima altura correspondiente a un tiro vertical

2.3 Cálculo de la rapidez mínima

Tenemos la relación para el alcance máximo en función de la rapidez

\ma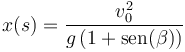 $x(s)= \frac{v_0^2}{g\left(1+\mathrm{sen}(\beta)\right)}$

Para que este valor sea D, la rapidez debe ser

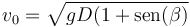
$v_0=\sqrt{gD(1+\mathrm{sen}(\beta)}$

3 Caso particular

3.1 Rapidez de lanzamiento

Si la pendiente es del 75% y la distancia es de 100 m, la rapidez en el momento del lanzamiento debe ser

$\mathrm{tg}(\beta)=0.75\qquad\Rightarrow\qquad \mathrm{sen}(\beta)=0.6\qquad\Rightarrow\qquad v_0=\sqrt{9.8\times 100\times\left(1+0.6\right)}\frac{\mathrm{m}}{\mathrm{s}}=39.6\,\frac{\mathrm{m}}{\mathrm{s}}$

@@ Línea 8: / Línea 8: @@
 ## La aceleración tangencial y normal (escalares) en el momento de impacto.
 Tómese <math>g\simeq 10\mathrm{m}/\mathrm{s}^2</math>.
-==rapidez mínima==
+==Rapidez mínima==
 La rápidez de lanzamiento mínima para llegar a un punto es aquella que tiene la distancia al punto como alcance máximo. Si no fuera así, siempre podría reducirse la rapidez de lanzamiento y llegar al mismo punto.
@@ Línea 88: / Línea 88: @@
 Tenemos la relación para el alcance máximo en función de la rapidez
-\max(s)= \frac{v_0^2}{g\left(1+\mathrm{sen}(\beta)\right)}
+\ma<center><math>x(s)= \frac{v_0^2}{g\left(1+\mathrm{sen}(\beta)\right)}</math></center>
 Para que este valor sea D, la rapidez debe ser
@@ Línea 94: / Línea 94: @@
 <center><math>v_0=\sqrt{gD(1+\mathrm{sen}(\beta)}</math></center>
+==Caso particular==
+===Rapidez de lanzamiento===
+Si la pendiente es del 75% y la distancia es de 100&#8202;m, la rapidez en el momento del lanzamiento debe ser
+<center><math>\mathrm{tg}(\beta)=0.75\qquad\Rightarrow\qquad \mathrm{sen}(\beta)=0.6\qquad\Rightarrow\qquad v_0=\sqrt{9.8\times 100\times\left(1+0.6\right)}\frac{\mathrm{m}}{\mathrm{s}}=39.6\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 [[Categoría:Problemas de cinemática tridimensional (GIE)]]

Tiro parabólico sobre una pendiente

De Laplace

Revisión de 10:30 8 oct 2017

Contenido

1 Enunciado

2 Rapidez mínima

2.1 Alcance general

2.2 Alcance máximo

2.3 Cálculo de la rapidez mínima

3 Caso particular

3.1 Rapidez de lanzamiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES