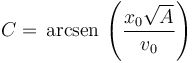Partícula con aceleración dependiente de x
De Laplace
(Página creada con '= Enunciado = Una partícula se desplaza sobre el eje <math>OX</math> de modo que su aceleración cumple en cada instante <math>a(x) = -Ax</math>, siendo <math>A</math> una cons…')
Edición más nueva →
Revisión de 17:05 2 oct 2017
1 Enunciado
Una partícula se desplaza sobre el eje OX de modo que su aceleración cumple en cada instante a(x) = − Ax, siendo A una constante. En la posición inicial la velocidad de la partícula es v0. Determina la función v(x).
2 Solución
La aceleración es
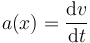
Introducimos la regla de la cadena multiplicando y dividiendo por dx
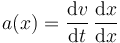
Como una derivada se puede entender como un cociente intercambiamos los dos números que aparecen en el denominador.
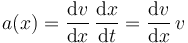
Hemos usado que v = dx / dt. Con esto nos ha quedado una ecuación diferencial en variables separables que se pueden integrar.
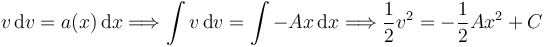
Imponiendo la condición inicial
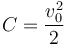
y por tanto
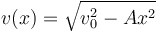
Ahora podemos plantear la ecuación diferencial para x(t)
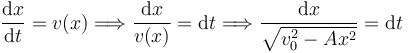
Para integrar hacemos el cambio
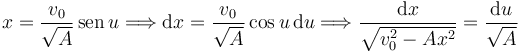
Integrando queda
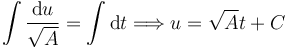
Y entonces
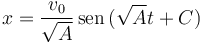
Si en t = 0 tenemos x = x0 nos queda