Entrar Página Discusión Historial Go to the site toolbox

Masa colgando de un hilo (GIE)

De Laplace

(Diferencias entre revisiones)
(→Enunciado)
(→Enunciado)
Línea 1: Línea 1:
==Enunciado==
==Enunciado==
Una partícula se halla situada en el extremo de un hilo de longitud <math>2b</math>, uno de cuyos extremos se encuentra en el punto <math>A(b,0)</math> y que pasa por una pequeña polea situada en el extremo de una barra de longitud <math>b</math> que gira alrededor del origen <math>O(0,0)</math> con velocidad angular constante <math>2\Omega</math>. En <math>t =0</math> la barra está completamente horizontal. La partícula cuelga verticalmente del hilo tras pasar éste por la polea y el movimiento es lo suficientemente lento como para que la partícula no oscile.
Una partícula se halla situada en el extremo de un hilo de longitud <math>2b</math>, uno de cuyos extremos se encuentra en el punto <math>A(b,0)</math> y que pasa por una pequeña polea situada en el extremo de una barra de longitud <math>b</math> que gira alrededor del origen <math>O(0,0)</math> con velocidad angular constante <math>2\Omega</math>. En <math>t =0</math> la barra está completamente horizontal. La partícula cuelga verticalmente del hilo tras pasar éste por la polea y el movimiento es lo suficientemente lento como para que la partícula no oscile.
-
<center>[[Archivo:barra-hilo.png]]</center>
+
<center>[[Archivo:barra-hilo.png|300px]]</center>
# Determine la posición, velocidad y aceleración de la partícula como función del tiempo.
# Determine la posición, velocidad y aceleración de la partícula como función del tiempo.
# Para el instante <math>t=\pi/(2\Omega)</math>, halle
# Para el instante <math>t=\pi/(2\Omega)</math>, halle

Revisión de 14:17 31 ago 2017

Contenido

1 Enunciado

Una partícula se halla situada en el extremo de un hilo de longitud 2b, uno de cuyos extremos se encuentra en el punto A(b,0) y que pasa por una pequeña polea situada en el extremo de una barra de longitud b que gira alrededor del origen O(0,0) con velocidad angular constante 2Ω. En t = 0 la barra está completamente horizontal. La partícula cuelga verticalmente del hilo tras pasar éste por la polea y el movimiento es lo suficientemente lento como para que la partícula no oscile.

  1. Determine la posición, velocidad y aceleración de la partícula como función del tiempo.
  2. Para el instante t = π / (2Ω), halle
    1. La posición, velocidad y aceleración de la partícula.
    2. El triedro de Frenet referido a la base canónica {i\vec{},j\vec{},k\vec{} }
    3. Las componentes intrínsecas de la aceleración (escalares).
    4. El radio y el centro de curvatura.

2 Posición, velocidad y aceleración

2.1 Posición

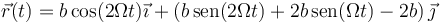
\vec{r}(t)=b\cos(2\Omega t)\vec{\imath}+\left(b\,\mathrm{sen}(2\Omega t)+2b\,\mathrm{sen}(\Omega t)-2b\right)\vec{\jmath}

2.2 Velocidad

\vec{v}(t)=-2b\Omega\,\mathrm{sen}(2\Omega t)\vec{\imath}+2b\Omega\left(\cos(2\Omega t)+\cos(\Omega t)\right)\vec{\jmath}

2.3 Aceleración

\vec{a}(t)=-4b\Omega^2\,\mathrm{cos}(2\Omega t)\vec{\imath}-2b\Omega^2\left(2\,\mathrm{sen}(2\Omega t)+\Omega\,\mathrm{sen}(\Omega t)\right)\vec{\jmath}

3 Instante t = π/2Ω

3.1 Posición, velocidad y aceleración

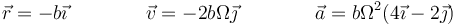
\vec{r}=-b\vec{\imath}\qquad\qquad \vec{v}=-2b\Omega\vec{\jmath}\qquad\qquad \vec{a}=b\Omega^2(4\vec{\imath}-2\vec{\jmath})

3.2 Triedro de Frenet

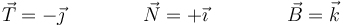
\vec{T}=-\vec{\jmath}\qquad\qquad \vec{N}=+\vec{\imath}\qquad\qquad \vec{B}=\vec{k}

3.3 Componentes intrínsecas

a_t=2b\Omega^2\qquad\qquad a_n = 4b\Omega^2

3.4 Radio y centro de curvatura

R=b\qquad\qquad \vec{r}_c=\vec{0}
Obtenido de "http://tesla.us.es/wiki/index.php/Masa_colgando_de_un_hilo_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace