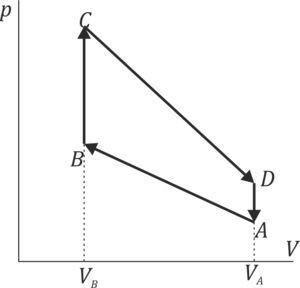
Ciclo termodinámico trapezoidal (GIE)
De Laplace
(Diferencias entre revisiones)
m (→Enunciado) |
|||
| Línea 5: | Línea 5: | ||
# Calcule el trabajo realizado sobre el sistema en el proceso A→B como función de la presión final <math>p_B</math> y del resto de datos del problema. | # Calcule el trabajo realizado sobre el sistema en el proceso A→B como función de la presión final <math>p_B</math> y del resto de datos del problema. | ||
# Halle el valor de la presión final <math>p_B</math> si en el proceso descrito el calor neto que entra en el sistema es nulo, <math>Q^{A\to B}=0</math>. | # Halle el valor de la presión final <math>p_B</math> si en el proceso descrito el calor neto que entra en el sistema es nulo, <math>Q^{A\to B}=0</math>. | ||
| - | # Halle la temperatura final T_B en el proceso anterior. | + | # Halle la temperatura final <math>T_B</math> en el proceso anterior. |
Suponga ahora un ciclo similar al Otto en el que el proceso A→B es el del apartado 2 y el C→D es del mismo tipo (<math>Q^{C\to D}=0</math>) con <math>T_C=1122\,\mathrm{K}</math>. Los procesos B→C y D→A son isócoros. | Suponga ahora un ciclo similar al Otto en el que el proceso A→B es el del apartado 2 y el C→D es del mismo tipo (<math>Q^{C\to D}=0</math>) con <math>T_C=1122\,\mathrm{K}</math>. Los procesos B→C y D→A son isócoros. | ||
<ol start="4"> | <ol start="4"> | ||
última version al 13:10 12 jun 2017
Contenido |
1 Enunciado
Una cierta cantidad de aire seco experimenta una compresión cuasiestática A→B que se describe en un diagrama pV con un segmento rectilíneo como el de la figura. Sean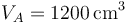 
, 
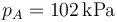y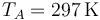 
las condiciones iniciales yVA / VB = r = 3 la relación de compresión
- Calcule el trabajo realizado sobre el sistema en el proceso A→B como función de la presión final pB y del resto de datos del problema.
- Halle el valor de la presión final pB si en el proceso descrito el calor neto que entra en el sistema es nulo,
.
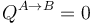- Halle la temperatura final TB en el proceso anterior.
Suponga ahora un ciclo similar al Otto en el que el proceso A→B es el del apartado 2 y el C→D es del mismo tipo (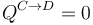
) con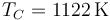 
. Los procesos B→C y D→A son isócoros.
- Halle la presión, temperatura y volumen de los estados A, B, C y D.
- Calcule el calor, el trabajo y la variación de la energía interna en cada uno de los procesos.
2 Trabajo para cualquier pB
Área de un trapecio
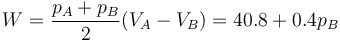
(pB en kPa, W en J)
3 Caso en el que Q = 0
Con el W anterior y con
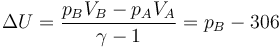
se hace
4 Temperatura en el estado B
Ley de los gases ideales
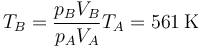
5 Valores de las funciones de estado
Aplicando la ley de los gases ideales o la relación del apartado 2 (análogamente para el proceso C→D)
| Estado | p (kPa) | V (L) | T (K) |
|---|---|---|---|
| A | 102 | 1.2 | 297 |
| B | 578 | 0.4 | 561 |
| C | 1156 | 0.4 | 1122 |
| D | 204 | 1.2 | 594 |
6 Calor, trabajo y energía interna
Aplicando repetidamente el primer principio de la termodinámica para gases ideales
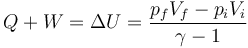
y que en cada paso o bien Q=0 o bien W=0, queda
| Proceso | Q (J) | W (J) | ΔU (J) |
|---|---|---|---|
| A→B | 0 | 272 | 272 |
| B→C | 578 | 0 | 578 |
| C→A | 0 | −544 | −544 |
| D→A | −306 | 0 | −306 |
