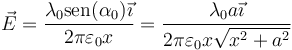Campo eléctrico de un segmento

De Laplace

(Diferencias entre revisiones)

Revisión de 21:40 28 mar 2017

Contenido

1 Enunciado
2 Segmento
3 Hilo infinito

1 Enunciado

Calcule el campo eléctrico producido por un segmento rectilíneo cargado uniformemente con una densidad de carga $λ 0$ en cualquier punto del plano perpendicular al segmento por su punto medio.

A partir del resultado anterior, halle el campo eléctrico creado por un hilo rectilíneo infinitamente largo cargado con una densidad homogénea $λ 0$ .

2 Segmento

El campo eléctrico creado por una distribución lineal de carga es

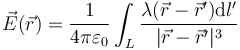
$\vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}\int_L\frac{\lambda(\vec{r}-\vec{r}')\mathrm{d}l'}{|\vec{r}-\vec{r}'|^3}$

En nuestro caso, situamos el segmento cargado en el eje OZ y centrado en el origen de coordenadas, de forma que los puntos donde se encuentran las cargas cumplen

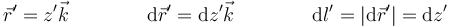
$\vec{r}'=z'\vec{k}\qquad \qquad \mathrm{d}\vec{r}'=\mathrm{d}z'\vec{k}\qquad\qquad \mathrm{d}l'=|\mathrm{d}\vec{r}'|=\mathrm{d}z'$

la variable $z'$ irá de $- a$ a $+ a$ .

Para los puntos donde medimos el campo nos dicen que se trata de un punto del plano central $z = 0$

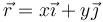
$\vec{r}=x\vec{\imath}+y\vec{\jmath}$

No obstante, dado que el sistema tiene simetría de revolución respecto al eje Z podemos considerar simplemente un punto del eje OX y luego generalizar. En este caso

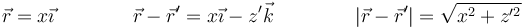
$\vec{r}=x\vec{\imath}\qquad\qquad \vec{r}-\vec{r}'=x\vec{\imath}-z'\vec{k}\qquad\qquad \left|\vec{r}-\vec{r}'\right|=\sqrt{x^2+z'^2}$

Llevando esto a la integral nos queda

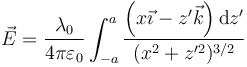
$\vec{E}=\frac{\lambda_0}{4\pi\varepsilon_0}\int_{-a}^a\frac{\left(x\vec{\imath}-z'\vec{k}\right)\mathrm{d}z'}{(x^2+z'^2)^{3/2}}$

Esta integral vectorial se descompone en dos integrales escalares. De éstas, la segunda se anula

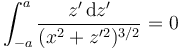
$\int_{-a}^a \frac{z'\,\mathrm{d}z'}{(x^2+z'^2)^{3/2}}=0$

por tratarse de una integral de una función impar sobre un intervalo simétrico. Esto nos deja con

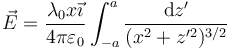
$\vec{E}=\frac{\lambda_0x\vec{\imath}}{4\pi\varepsilon_0}\int_{-a}^a\frac{\mathrm{d}z'}{(x^2+z'^2)^{3/2}}$

Esta integral se resuelve mediante el cambio de variable

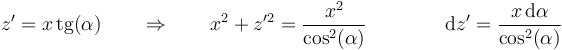
$z'=x\,\mathrm{tg}(\alpha)\qquad\Rightarrow\qquad x^2+z'^2 = \frac{x^2}{\cos^2(\alpha)}\qquad\qquad \mathrm{d}z'=\frac{x\,\mathrm{d}\alpha}{\cos^2(\alpha)}$

Este ángulo posee una interpretación geométrica: es el ángulo de elevación respecto a la horizontal con el que se ve un punto del segmento desde la posición donde queremos hallar el campo. Con este cambio de variable la integral se transforma en

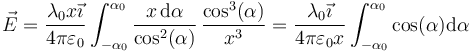
$\vec{E}=\frac{\lambda_0 x\vec{\imath}}{4\pi\varepsilon_0}\int_{-\alpha_0}^{\alpha_0}\frac{x\,\mathrm{d}\alpha}{\cos^2(\alpha)}\,\frac{\cos^3(\alpha)}{x^3}=\frac{\lambda_0\vec{\imath}}{4\pi\varepsilon_0 x}\int_{-\alpha_0}^{\alpha_0}\cos(\alpha)\mathrm{d}\alpha$

El límite de integración lo da el ángulo de elevación del extremo del segmento

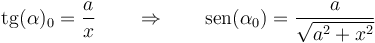
$\mathrm{tg}(\alpha)_0=\frac{a}{x}\qquad\Rightarrow\qquad \mathrm{sen}(\alpha_0)=\frac{a}{\sqrt{a^2+x^2}}$

Con esto, la expresión para el campo eléctrico queda

$\vec{E}=\frac{\lambda_0 \mathrm{sen}(\alpha_0)\vec{\imath}}{2\pi\varepsilon_0 x}=\frac{\lambda_0 a\vec{\imath}}{2\pi\varepsilon_0 x\sqrt{x^2+a^2}}$

3 Hilo infinito

@@ Línea 25: / Línea 25: @@
 Llevando esto a la integral nos queda
-<center><math>\vec{E}=\frac{\lambda_0}{4\pi\varepsilon_0}\int_{-a}^a\frac{(x\vec{\imath}-z'\vec{k})\mathrm{d}z'}{(x^2+z'^2)^{3/2}}</math></center>
+<center><math>\vec{E}=\frac{\lambda_0}{4\pi\varepsilon_0}\int_{-a}^a\frac{\left(x\vec{\imath}-z'\vec{k}\right)\mathrm{d}z'}{(x^2+z'^2)^{3/2}}</math></center>
 Esta integral vectorial se descompone en dos integrales escalares. De éstas, la segunda se anula
-<center><math>\int_{-a}^a \frac{z'\,\mathrm{d}z'}{(x^2+z'^2)^{3/2}}</math></center>
+<center><math>\int_{-a}^a \frac{z'\,\mathrm{d}z'}{(x^2+z'^2)^{3/2}}=0</math></center>
 por tratarse de una integral de una función impar sobre un intervalo simétrico. Esto nos deja con

Campo eléctrico de un segmento

De Laplace

Revisión de 21:40 28 mar 2017

Contenido

1 Enunciado

2 Segmento

3 Hilo infinito

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES