Oscilador no lineal
De Laplace
(Diferencias entre revisiones)
(→Energía potencial) |
(→Energía mecánica) |
||
| Línea 47: | Línea 47: | ||
<center><math> E = T + U = \frac{1}{2}mv^2 - \frac{cx^2}{2}+\frac{px^4}{4}</math></center> | <center><math> E = T + U = \frac{1}{2}mv^2 - \frac{cx^2}{2}+\frac{px^4}{4}</math></center> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
===Movimiento periódico=== | ===Movimiento periódico=== | ||
Revisión de 13:18 8 feb 2009
Contenido[ocultar] |
1 Enunciado
Una partícula está sometida exclusivamente a una fuerza, dependiente de la posición, dada por
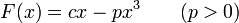
- Halle la expresión de la energía potencial y la energía mecánica para la partícula. Esboce las gráficas para los casos c < 0 y c > 0.
- Demuestre que el movimiento de la partícula siempre es acotado, y periódico.
- Localice las posiciones de equilibrio de la partícula (a) si c < 0 (b) si c > 0.
- Suponga que la partícula se suelta desde una posición muy próxima a las posiciones de equilibrio calculadas en el apartado anterior. ¿En qué caso describe oscilaciones? Halle el valor aproximado del periodo de oscilación para este movimiento.
2 Solución
2.1 Energía mecánica
2.1.1 Energía potencial
Esta fuerza, dependiente solo de la posición, es una fuerza conservativa, que deriva de una energía potencial. Podemos calcular esta energía observando que el trabajo realizado por esta fuerza corresponde a una disminución de la energía potencial
Hallando la integral obtenemos la energía potencial
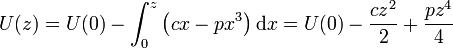
Si tomamos como origen de energía potencial el centro del sistema (z = 0) nos queda finalmente (llamando x a la variable):
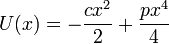
La curva para esta energía potencial tiene las siguientes propiedades:
- Es una función par. Puesto que solo aparecen potencias pares, la gráfica de U(x) es simétrica, esto es
- Tiende a
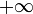para 
. Cuando x es grande, el término en x4 domina sobre x2 (por ejemplo, para x = 1000, x2 es 1 millón y x4 es 1 billón. Esto quiere decir que si nos alejamos lo suficiente de la posición central la energía potencial va creciendo progresivamente.
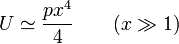
- Puesto que la energía mecánica de una partícula es una cantidad finita, esta propiedad implicará, como veremos, que el movimiento debe ser periódico.
- Puede tener un máximo o un mínimo en x = 0. Cuando x es pequeño, x2 es mucho más grande que x4 (para x una décima, x2 es sólo una centésima, pero x4 es aun menor, una diezmilésima). Por ello, cerca del punto central
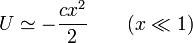
- Si c < 0, la curva es aproximadamente una parábola hacia arriba, y el punto central es un mínimo (la segunda derivada es positiva). Si c > 0, la parábola es hacia abajoy la curva posee un máximo. En combinación con la propiedad anterior, esto significa que habrá dos mínimos adicionales, uno a cada lado.
2.1.2 Energía mecánica
La energía mecánica es la suma de la energía cinética y de la potencial que acabamos de calcular
