Plataforma sobre cilindro rodante (GIE)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Un rodillo cilíndrico macizo homogéneo de masa <math>m</math> y radio <math>R</math> puede rodar sin deslizar sobre una superficie horizontal. El rodillo se encu…') |
|||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| + | [[Archivo:plataforma-rodillo.png|400px|right]] | ||
| + | |||
Un rodillo cilíndrico macizo homogéneo de masa <math>m</math> y radio <math>R</math> puede rodar sin deslizar sobre una superficie horizontal. El rodillo se encuentra impulsado por una fina plataforma horizontal de masa <math>m_0</math> cuyo contacto con el rodillo es también de rodadura sin deslizamiento. En un instante dado en que la plataforma está centrada sobre el rodillo y el sistema se halla en reposo se tira de ella con una fuerza <math>\vec{F}_0=F_0 \vec{\imath}</math>. Determine, en el orden que estime necesario: | Un rodillo cilíndrico macizo homogéneo de masa <math>m</math> y radio <math>R</math> puede rodar sin deslizar sobre una superficie horizontal. El rodillo se encuentra impulsado por una fina plataforma horizontal de masa <math>m_0</math> cuyo contacto con el rodillo es también de rodadura sin deslizamiento. En un instante dado en que la plataforma está centrada sobre el rodillo y el sistema se halla en reposo se tira de ella con una fuerza <math>\vec{F}_0=F_0 \vec{\imath}</math>. Determine, en el orden que estime necesario: | ||
* La aceleración angular del rodillo, la aceleración del centro del rodillo, y la aceleración de la plataforma. | * La aceleración angular del rodillo, la aceleración del centro del rodillo, y la aceleración de la plataforma. | ||
Revisión de 21:26 8 feb 2017
Enunciado
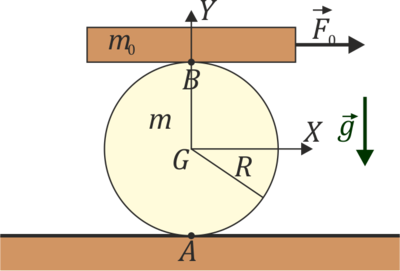
Un rodillo cilíndrico macizo homogéneo de masa m y radio R puede rodar sin deslizar sobre una superficie horizontal. El rodillo se encuentra impulsado por una fina plataforma horizontal de masa m0 cuyo contacto con el rodillo es también de rodadura sin deslizamiento. En un instante dado en que la plataforma está centrada sobre el rodillo y el sistema se halla en reposo se tira de ella con una fuerza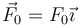 
. Determine, en el orden que estime necesario:
- La aceleración angular del rodillo, la aceleración del centro del rodillo, y la aceleración de la plataforma.
- Las fuerzas que actúan sobre el rodillo en el punto A, de contacto con el suelo y el punto B, donde se apoya la plataforma.
- Si el coeficiente de rozamiento estático entre el rodillo y el suelo, y entre el rodillo y la plataforma, vale μ, ¿cuál es valor máximo de F0 para que el rodillo no deslice? ¿Por dónde empezará a deslizar?
