Leyes de conservación en mecánica analítica (CMR)
De Laplace
| Línea 15: | Línea 15: | ||
==Coordenadas cíclicas== | ==Coordenadas cíclicas== | ||
| + | Suponemos el caso más simple de coordenadas generalizadas independientes y ausencia de fuerzas no conservativas. En estas condiciones se satisfacen las ecuaciones de Lagrange | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial\mathcal{L}}{\partial \dot{q}_k}\right)-\frac{\partial \mathcal{L}}{\partial q_k}=0</math></center> | ||
| + | |||
| + | siendo la lagrangiana del sistema | ||
| + | |||
| + | <center><math>\mathcal{L}(q_k,\dot{q}_k,t)=K-U</math></center> | ||
| + | |||
| + | Una coordenada <math>q_1</math> se dice <math>cíclica</math> o <math>ignorable</math> si no aparece en la lagrangiana, es decir | ||
| + | |||
| + | <center><math>\mathcal{L}(q_2,\ldots,q_n,\dot{q}_1\,\ldots,\dot{q}_n,t)</math></center> | ||
| + | |||
| + | y por tanto se anula derivada parcial | ||
| + | |||
| + | <center><math>\frac{\partial\mathcal{L}}{\partial q_1}=0</math></center> | ||
| + | |||
| + | Esto implica, de acuerdo con las ecuaciones de Lagrange, que | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial\mathcal{L}}{\partial \dot{q}_k}\right)=0\qquad\Rightarrow\qquad \frac{\partial\mathcal{L}}{\partial \dot{q}_1}=\beta_1 = \mathrm{cte}</math></center> | ||
| + | |||
| + | A la derivada parcial | ||
| + | |||
| + | <center><math>p_j=\frac{\partial\mathcal{L}}{\partial \dot{q}_j}(q_k,\dot{q}_k,t)</math></center> | ||
| + | |||
| + | se la denomina el ''momento conjugado'' de la coordenada <math>q_j</math>. Por tanto, si <math>q_1</math> es cíclica su momento conjugado <math>p_1</math> es una constante de movimiento de valor <math>\beta_1</math> dado por las condiciones iniciales. | ||
| + | |||
| + | Hay una estrecha relación entre las constantes de movimiento y las simetrías del sistema. | ||
| + | |||
| + | * En el caso de que <math>q_1</math> represente una coordenada cartesiana, su momento conjugado representa la cantidad de movimiento en dicha dirección. Por tanto, si el sistema tiene ''simetría traslacional'', es decir, no cambia al realizar un desplzamiento rectilíneo, entonces se conserva una componente de la cantidad de movimiento. | ||
| + | |||
| + | * En el caso de que <math>q_1</math> represente una coordenada angular en torno a un eje, su momento conjugado representa el momento cinético asociado a giros en torno al eje. Por tanto, si el sistema tiene ''simetría de revolución'', es decir, no cambia al realizar un desplzamiento en torno al eje, entonces se conserva una componente del momento cinético. | ||
| + | |||
==Función de Routh== | ==Función de Routh== | ||
==Energía y función hamiltoniana== | ==Energía y función hamiltoniana== | ||
[[Categoría:Mecánica analítica (CMR)]] | [[Categoría:Mecánica analítica (CMR)]] | ||
Revisión de 01:07 17 ene 2017
Contenido |
1 Introducción
Una constante de movimiento o integral primera es una función dependiente de las coordenadas, velocidades y posiblemente el tiempo, cuyo valor es el mismo en todo instante.
Si el sistema viene descrito por una serie de coordenadas generalizadas qk, una constante de movimiento cumpliría
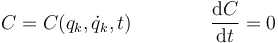
Desarrollando aquí la derivada total queda la condición para que C sea una constante
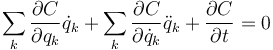
A partir de las ecuaciones de Lagrange pueden obtenerse expresiones para las segundas derivadas que, sustituidas aquí deberían llevar a la anulación del primer término, si efectivamente C es una constante.
La búsqueda de constantes de movimiento es una tarea que puede ser complicada, ya que las posibles combinaciones de coordenadas generalizadas son infinitas. Aquí conideraremos solo los casos matemáticamente más simples.
2 Coordenadas cíclicas
Suponemos el caso más simple de coordenadas generalizadas independientes y ausencia de fuerzas no conservativas. En estas condiciones se satisfacen las ecuaciones de Lagrange
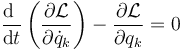
siendo la lagrangiana del sistema
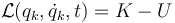
Una coordenada q1 se dice cclica o ignorable si no aparece en la lagrangiana, es decir
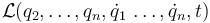
y por tanto se anula derivada parcial
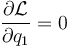
Esto implica, de acuerdo con las ecuaciones de Lagrange, que
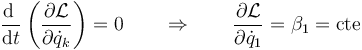
A la derivada parcial
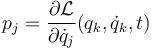
se la denomina el momento conjugado de la coordenada qj. Por tanto, si q1 es cíclica su momento conjugado p1 es una constante de movimiento de valor β1 dado por las condiciones iniciales.
Hay una estrecha relación entre las constantes de movimiento y las simetrías del sistema.
- En el caso de que q1 represente una coordenada cartesiana, su momento conjugado representa la cantidad de movimiento en dicha dirección. Por tanto, si el sistema tiene simetría traslacional, es decir, no cambia al realizar un desplzamiento rectilíneo, entonces se conserva una componente de la cantidad de movimiento.
- En el caso de que q1 represente una coordenada angular en torno a un eje, su momento conjugado representa el momento cinético asociado a giros en torno al eje. Por tanto, si el sistema tiene simetría de revolución, es decir, no cambia al realizar un desplzamiento en torno al eje, entonces se conserva una componente del momento cinético.





