Colisión de dos osciladores armónicos (GIE)
De Laplace
(Diferencias entre revisiones)
| Línea 11: | Línea 11: | ||
<li>¿Qué proporción de la energía inicial se ha perdido en la colisión?</li> | <li>¿Qué proporción de la energía inicial se ha perdido en la colisión?</li> | ||
<li>¿Cuál es la amplitud de las oscilaciones que experimenta el conjunto tras el choque?</li> | <li>¿Cuál es la amplitud de las oscilaciones que experimenta el conjunto tras el choque?</li> | ||
| + | </ol> | ||
==Velocidad antes del impacto== | ==Velocidad antes del impacto== | ||
Revisión de 17:17 12 dic 2016
Contenido |
1 Enunciado
Sobre una superficie horizontal sin rozamiento se encuentran dos masas aproximadamente puntuales, de valores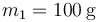 
y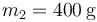 
. Las masas están unidas a paredes enfrentadas (las cuales distan 
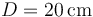) mediante dos resortes de longitud natural 
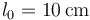y constantes 
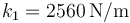y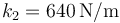 
, respectivamente.
Estando las dos masas en reposo en la posición central, se desplaza m1 hacia la izquierda, comprimiendo el muelle 1 una cantidad 
. Desde ahí se suelta.
- Calcule la velocidad de la masa 1 justo antes de que impacte con la 2.
- Si el choque es completamente elástico, halle la velocidad de cada masa tras la colisión.
- Calcule la máxima distancia de la posición central a la que llega cada masa en la oscilación posterior.
Suponga ahora que la colisión es completamente inelástica, quedando soldadas las dos masas
- ¿Cuál es la velocidad del conjunto justo tras la colisión?
- ¿Qué proporción de la energía inicial se ha perdido en la colisión?
- ¿Cuál es la amplitud de las oscilaciones que experimenta el conjunto tras el choque?
2 Velocidad antes del impacto
3 Velocidades tras la colisión
4 Amplitudes tras la colisión
5 Velocidad tras la colisión inelástica
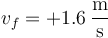
6 Pérdida de energía
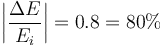
7 Amplitud tras la colisión inelástica
