Partícula girando suspendida de un hilo
De Laplace
(Diferencias entre revisiones)
| Línea 2: | Línea 2: | ||
Una partícula de masa <math>m</math> gira horizontalmente con rapidez <math>v_0</math>, atada a un hilo inextensible y sin masa de longitud <math>b</math>. El hilo forma un ángulo constante <math>\theta</math> con la vertical. En <math>t=0</math> la partícula se encuentra en el plano OXZ, según los ejes indicados en la figura. | Una partícula de masa <math>m</math> gira horizontalmente con rapidez <math>v_0</math>, atada a un hilo inextensible y sin masa de longitud <math>b</math>. El hilo forma un ángulo constante <math>\theta</math> con la vertical. En <math>t=0</math> la partícula se encuentra en el plano OXZ, según los ejes indicados en la figura. | ||
| - | <center>[[Archivo:particula-extremo-hilo.png]]</center> | + | <center>[[Archivo:particula-extremo-hilo.png|400px]]</center> |
# Exprese las ecuaciones horarias del movimiento: <math>x(t)</math>, <math>y(t)</math> y <math>z(t)</math>. | # Exprese las ecuaciones horarias del movimiento: <math>x(t)</math>, <math>y(t)</math> y <math>z(t)</math>. | ||
# Calcule el valor de <math>v_0</math> así como la tensión del hilo, en función del ángulo <math>\theta</math> (y <math>m</math>, <math>g</math> y <math>b</math>). Si el hilo soporta una tensión máxima <math>F_max=3mg</math>, que si se supera se rompe, ¿cuál es la rapidez máxima que le podemos comunicar a la masa sin que se rompa el hilo? | # Calcule el valor de <math>v_0</math> así como la tensión del hilo, en función del ángulo <math>\theta</math> (y <math>m</math>, <math>g</math> y <math>b</math>). Si el hilo soporta una tensión máxima <math>F_max=3mg</math>, que si se supera se rompe, ¿cuál es la rapidez máxima que le podemos comunicar a la masa sin que se rompa el hilo? | ||
# Calcule la energía mecánica de la partícula como función de <math>\theta</math> (y <math>m</math>, <math>g</math> y <math>b</math>, pero no <math>v_0</math>). Tómese como origen de energía potencial el punto O de anclaje del hilo | # Calcule la energía mecánica de la partícula como función de <math>\theta</math> (y <math>m</math>, <math>g</math> y <math>b</math>, pero no <math>v_0</math>). Tómese como origen de energía potencial el punto O de anclaje del hilo | ||
# Calcule el momento cinético de la partícula respecto al punto O como función de <math>\theta</math> y del tiempo (y <math>m</math>, <math>g</math> y <math>b</math>, pero no <math>v_0</math>). ¿Es constante alguna de sus componentes? | # Calcule el momento cinético de la partícula respecto al punto O como función de <math>\theta</math> y del tiempo (y <math>m</math>, <math>g</math> y <math>b</math>, pero no <math>v_0</math>). ¿Es constante alguna de sus componentes? | ||
| + | |||
| + | ==Ecuaciones horarias== | ||
| + | La partícula tiene una altura constante, ya que gira horizontalmente | ||
| + | |||
| + | <center><math>z=-b\,\mathrm{sen}(\theta)</math></center> | ||
| + | |||
| + | Su movimiento es circular, siendo el radio de la circunferencia <math>R=b\cos(\theta\,)</math>. La partícula se mueve con rapidez constante <math>v_0</math> por lo que su periodo de revolución sale de | ||
| + | |||
| + | <center><math>v_0=\frac{2\pi R}{T}\qquad\Rightarrow\qquad T = \frac{2\pi b\cos(\theta)}{v_0}</math></center> | ||
| + | |||
| + | y por tanto la velocidad angular vale | ||
| + | |||
| + | <center><math>\omega = \frac{2\pi}{T}=\frac{v_0}{b\cos(\theta)}</math></center> | ||
| + | |||
| + | lo que nos da las ecuaciones horarias restantes | ||
| + | |||
| + | <center><math>x = R\cos(\omega t)=b\cos(\theta)\cos\left(\frac{v_0 t}{b\cos(\theta)}\right)\qquad\qquad y = R\,\mathrm{sen}(\omega t)=b\cos(\theta)\,\mathrm{sen}\left(\frac{v_0 t}{b\cos(\theta)}\right)</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==Velocidad y tensión== | ||
| + | ==Energía mecánica== | ||
| + | ==Momento cinético== | ||
Revisión de 22:54 12 sep 2016
Contenido |
1 Enunciado
Una partícula de masa m gira horizontalmente con rapidez v0, atada a un hilo inextensible y sin masa de longitud b. El hilo forma un ángulo constante θ con la vertical. En t = 0 la partícula se encuentra en el plano OXZ, según los ejes indicados en la figura.
- Exprese las ecuaciones horarias del movimiento: x(t), y(t) y z(t).
- Calcule el valor de v0 así como la tensión del hilo, en función del ángulo θ (y m, g y b). Si el hilo soporta una tensión máxima Fmax = 3mg, que si se supera se rompe, ¿cuál es la rapidez máxima que le podemos comunicar a la masa sin que se rompa el hilo?
- Calcule la energía mecánica de la partícula como función de θ (y m, g y b, pero no v0). Tómese como origen de energía potencial el punto O de anclaje del hilo
- Calcule el momento cinético de la partícula respecto al punto O como función de θ y del tiempo (y m, g y b, pero no v0). ¿Es constante alguna de sus componentes?
2 Ecuaciones horarias
La partícula tiene una altura constante, ya que gira horizontalmente
Su movimiento es circular, siendo el radio de la circunferencia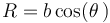 
. La partícula se mueve con rapidez constante v0 por lo que su periodo de revolución sale de
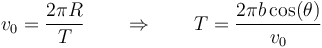
y por tanto la velocidad angular vale
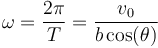
lo que nos da las ecuaciones horarias restantes
