Dos hemisferios y una lámina conductora
De Laplace
(→Enunciado) |
(→Cargas y potenciales) |
||
| Línea 13: | Línea 13: | ||
==Solución== | ==Solución== | ||
===Cargas y potenciales=== | ===Cargas y potenciales=== | ||
| + | Este sistema está formado por solo dos conductores, ya que las semiesferas están conectadas en todo momento, de forman que se comportan de forma solidaria. llmamaremos “1” a la placa central y “2” a la asociación de los dos hemisferios. | ||
| + | |||
| + | La matriz de coeficientes de capacidad tendrá tres elementos independientes | ||
| + | |||
| + | <center><math>\mathsf{C}=\begin{pmatrix}C_{11} & C_{12}\\ C_{12} & C_{22}\end{pmatrix</math></center> | ||
| + | |||
| + | Estos coeficientes pueden calcularse a partir del circuito equivalente, el cual estará formado, en principio por tres condensadores. | ||
| + | |||
| + | El condensador <math>\overline{C}_{12}</math> es el que forma la placa central con las dos semiesferas. Su capacidad corresponde a la asociación en paralelo de dos condensadores planos, de sección <math>\pi R^2</math> y distancia entre placas <math>a</math>. Por ello, | ||
| + | |||
| + | <center><math>\overline{C}_{12}= \frac{2\varepsilon_0 \pi R^2}{a}</math></center> | ||
| + | |||
| + | El condensador <math>\overline{C}_{11}</math> corresponde a las líneas de campo que van de la placa central a tierra (el infinito). Sin embargo, si despreciamos los efectos de borde, todas las líneas de campo del conductor 1 van a parar al 2, esto es, el 1 se encuentra en influencia total con el 2. Al no haber líneas que vayan del 1 al infinito | ||
| + | |||
| + | <center><math>\overline{C}_{11} = 0</math></center> | ||
| + | |||
===Campo eléctrico=== | ===Campo eléctrico=== | ||
===Energía electrostática=== | ===Energía electrostática=== | ||
Revisión de 17:44 14 ene 2009
Contenido |
1 Enunciado
Se tiene un sistema formado por dos conductores hemisféricos de radio R. Estas dos semiesferas están separadas una pequeña distancia 2a (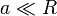 ). En el espacio entre las dos semiesferas se encuentra una fina chapa circular de radio R y separada una distancia a de cada hemisferio.
). En el espacio entre las dos semiesferas se encuentra una fina chapa circular de radio R y separada una distancia a de cada hemisferio.
Las dos semiesferas están conectadas por un hilo conductor en todo momento.
- Suponga que la chapa se encuentra a una tensión V0 mientras que el conjunto de las dos semiesferas está aislado y descargado. ¿Cuánto valen la cargas almacenadas y las tensiones de cada conductor?
- Para el caso anterior de las expresiones aproximadas para el campo entre la chapa y los hemisferios, y en el exterior de estos.
- Calcule la energía electrostática almacenada en este sistema.
- Suponga que se desconecta la fuente V0 y, acto seguido, se ponen los hemisferios a tierra. ¿Cuáles son las nuevas cargas, tensiones y energía almacenada?
Desprecie los efectos de borde.
2 Solución
2.1 Cargas y potenciales
Este sistema está formado por solo dos conductores, ya que las semiesferas están conectadas en todo momento, de forman que se comportan de forma solidaria. llmamaremos “1” a la placa central y “2” a la asociación de los dos hemisferios.
La matriz de coeficientes de capacidad tendrá tres elementos independientes
Estos coeficientes pueden calcularse a partir del circuito equivalente, el cual estará formado, en principio por tres condensadores.
El condensador 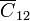 es el que forma la placa central con las dos semiesferas. Su capacidad corresponde a la asociación en paralelo de dos condensadores planos, de sección πR2 y distancia entre placas a. Por ello,
es el que forma la placa central con las dos semiesferas. Su capacidad corresponde a la asociación en paralelo de dos condensadores planos, de sección πR2 y distancia entre placas a. Por ello,
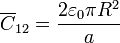
El condensador 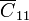 corresponde a las líneas de campo que van de la placa central a tierra (el infinito). Sin embargo, si despreciamos los efectos de borde, todas las líneas de campo del conductor 1 van a parar al 2, esto es, el 1 se encuentra en influencia total con el 2. Al no haber líneas que vayan del 1 al infinito
corresponde a las líneas de campo que van de la placa central a tierra (el infinito). Sin embargo, si despreciamos los efectos de borde, todas las líneas de campo del conductor 1 van a parar al 2, esto es, el 1 se encuentra en influencia total con el 2. Al no haber líneas que vayan del 1 al infinito







