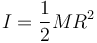Aro centrado en el origen (MR G.I.C.)
De Laplace
(Página creada con '== Enunciado == right Tenemos un aro homogéneo de masa <math>M</math> y radio <math>R</math> con centro <math>O</math>. Se escogen los e…')
Edición más nueva →
Revisión de 18:53 28 oct 2015
1 Enunciado
Tenemos un aro homogéneo de masa M y radio R con centro O. Se escogen los ejes coordenadas como se indica en la figura.
- Calcula la matriz de inercia en O, usando los ejes indicados en la figura.
- Calcula el momento de inercia respecto a un eje que pasa por O y forma un ángulo de π / 3 con el eje OX3.
2 Solución
2.1 Tensor de inercia
La forma general del tensor de inercia en un punto es
![\overleftrightarrow{I_O}
=
\left[
\begin{array}{ccc}
I_{11} & -P_{12} & -P_{13}\\
-P_{12} & I_{22} & -P_{23}\\
-P_{13} & -P_{23} & I_{33}
\end{array}
\right]](/wiki/images/math/b/6/3/b63facb02d61f94b9b95852045842865.png)
Ya hemos usado que el tensor es simétrico. Vamos a calcular primero los elementos no diagonales.
Tenemos
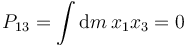
Esta integral se anula porque para todos los puntos del aro se cumple x3 = 0. Por la misma razón tenemos
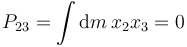
Para el otro producto de inercia
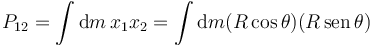
Tenemos
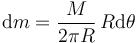
por lo que
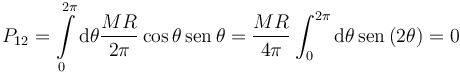
Los tres productos de inercia son cero. Este resultado se puede obtener sin hacer cuentas con argumentos de simetría. Al ser el aro un sólido plano, el eje X3 es principal de inercia, pues es perpendicular al plano del sólido. Y como el aro tiene simetría de revolución alrededor de X3, todas las direcciones perpendiculares a X3 que pasen por O son principales de inercia, en particular X1 y X2. Entonces, el tensor de inercia es diagonal respecto a los tres ejes indicados.
Vamos con los momentos de inercia. Al ser un sistema plano tenemos
I33 = I11 + I22
Y por la simetría del aro tenemos

Basta entonces con calcular I33.
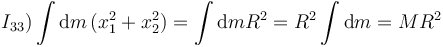
Todos los puntos están a la misma distancia del eje X3, el radio del aro R. Y la integral que queda es la masa total del aro.
Entonces el tensor de inercia en O es
![\overleftrightarrow{I_O}
=
I
\left[
\begin{array}{ccc}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 2
\end{array}
\right]](/wiki/images/math/8/6/8/86804d38474a997a6273f8f9077b6c0f.png)
con