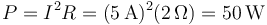Circuito con dos condensadores y una resistencia
De Laplace
| Línea 38: | Línea 38: | ||
<center><math>I=\frac{\Delta V}{R}=\frac{V_1-V_2}{R}=5\,\mathrm{A}</math></center> | <center><math>I=\frac{\Delta V}{R}=\frac{V_1-V_2}{R}=5\,\mathrm{A}</math></center> | ||
| + | |||
==Energía y potencia iniciales== | ==Energía y potencia iniciales== | ||
| + | La energía almacenada inicialmente es la suma de la que se guarda en cada condensador | ||
| + | |||
| + | <center><math>U_{\mathrm{e}i}=\frac{1}{2}C_1V_1^2 + \frac{1}{2}C_2V_2^2=1.80\,\mu\mathrm{J}+0.15\,\mu\mathrm{J}= 1.95\,\mu\mathrm{J}</math></center> | ||
| + | |||
| + | La potencia disipada la calculamos por la ley de Joule | ||
| + | |||
| + | <center><math>P=I^2R=(5\,\mathrm{A})^2(2\,\Omega)=50\,\mathrm{W}</math></center> | ||
| + | |||
==Cargas y potencias finales== | ==Cargas y potencias finales== | ||
==Energía almacenada final== | ==Energía almacenada final== | ||
==Balance energético== | ==Balance energético== | ||
[[Categoría:Problemas de corriente eléctrica (GIE)]] | [[Categoría:Problemas de corriente eléctrica (GIE)]] | ||
Revisión de 20:49 10 sep 2015
Contenido |
1 Enunciado
Se tiene un sistema mostrado en la figura, en el que los condensadores son de placas circulares, planas y paralelas de radio 18 cm. El condensador 1 tiene una distancia entre placas de 0.1 mm y el 2 una distancia de 0.3 mm. Ambos condensadores están rellenos de aire (equivalente al vacío). La conexión entre los condensadores se efectúa a través de un cable de 120 m de hilo de cobre de 1 mm² de sección.
Inicialmente el interruptor está cerrado y los condensadores están conectados a sendas fuentes de tensión ideales, que fijan voltajes 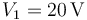 y
y 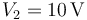 .
.
Para este instante, calcule
- La carga de cada condensador y la corriente que circula por el cable.
- La energía almacenada en los condensadores y la potencia disipada en la resistencia.
En un cierto momento, se abre el interruptor, desconectando la fuente 2. Se espera el tiempo necesario para que se vuelva a alcanzar el equilibrio.
- Halle las cargas de los condensadores y la corriente por la resistencia una vez que se ha llegado de nuevo al equilibrio.
- Calcule la energía almacenada en los condensadores en el estado final.
- Calcule el trabajo realizado por las fuentes de tensión y la energía disipada en el hilo desde que se abre el interruptor hasta el estado final.
2 Cargas y corrientes iniciales
Calculamos en primer lugar las capacidades de los condensadores y el valor de la resistencia.
Para cada condensador

lo que da

Cada condensador está conectado a su respectiva fuente de tensión, por lo que la carga de cada uno es

La resistencia del cable es
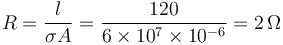
y la corriente que circula por él la da la ley de ohm
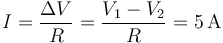
3 Energía y potencia iniciales
La energía almacenada inicialmente es la suma de la que se guarda en cada condensador
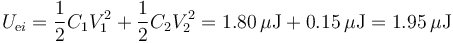
La potencia disipada la calculamos por la ley de Joule