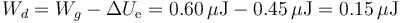Circuito con dos condensadores y una resistencia
De Laplace
Contenido |
1 Enunciado
Se tiene un sistema mostrado en la figura, en el que los condensadores son de placas circulares, planas y paralelas de radio 18 cm. El condensador 1 tiene una distancia entre placas de 0.1 mm y el 2 una distancia de 0.3 mm. Ambos condensadores están rellenos de aire (equivalente al vacío). La conexión entre los condensadores se efectúa a través de un cable de 120 m de hilo de cobre de 1 mm² de sección.
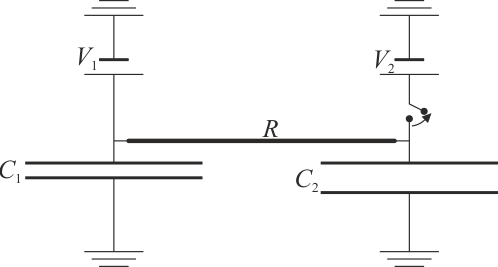
Inicialmente el interruptor está cerrado y los condensadores están conectados a sendas fuentes de tensión ideales, que fijan voltajes 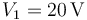 y
y 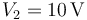 .
.
Para este instante, calcule
- La carga de cada condensador y la corriente que circula por el cable.
- La energía almacenada en los condensadores y la potencia disipada en la resistencia.
En un cierto momento, se abre el interruptor, desconectando la fuente 2. Se espera el tiempo necesario para que se vuelva a alcanzar el equilibrio.
- Halle las cargas de los condensadores y la corriente por la resistencia una vez que se ha llegado de nuevo al equilibrio.
- Calcule la energía almacenada en los condensadores en el estado final.
- Calcule el trabajo realizado por las fuentes de tensión y la energía disipada en el hilo desde que se abre el interruptor hasta el estado final.
2 Cargas y corrientes iniciales
Calculamos en primer lugar las capacidades de los condensadores y el valor de la resistencia.
Para cada condensador

lo que da

Cada condensador está conectado a su respectiva fuente de tensión, por lo que la carga de cada uno es

La resistencia del cable es
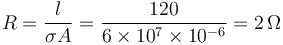
y la corriente que circula por él desde la fuente 1 a la fuente 2 la da la ley de Ohm
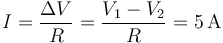
3 Energía y potencia iniciales
La energía almacenada inicialmente es la suma de la que se guarda en cada condensador
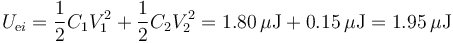
La potencia disipada la calculamos por la ley de Joule
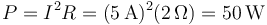
4 Cargas y corriente finales
Cuando se abre el interruptor, el condensador 2 deja de estar conectado a la fuente 2. Como inicialmente sigue existiendo una diferencia de potencial entre los extremos del cable, se mantiene la corriente por él, pero las cargas que transporta ya no se van por la fuente 2, sino que se almacenan el condensador 2.
El equilibrio se alcanza cuando desaparece la diferencia de potencial entre los extremos del cable, esto es, cuando
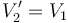
La d.d.p. entre las placas del condensador 1 no se ve afectada, por lo que
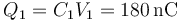
mientras que la carga final en el condensador 2 la da el nuevo potencial de su placa positiva

En el estado final no hay diferencia de potencial entre los extremos del cable, con lo que no fluye corriente alguna por él
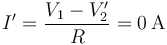
5 Energía almacenada final
En el estado final la energía almacenada se calcula de la misma manera que con la inicial
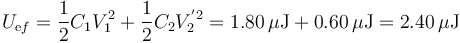
lo que da un incremento en la energía almacenada
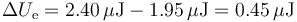
6 Balance energético
El trabajo realizado por una fuente de tensión continua es el producto de su tensión por la carga que pasa por la fuente
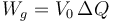
La fuente 2 no realiza trabajo ya que una vez desconectada por ella no pasa carga alguna.

Por la fuente 1 pasa la diferencia entre la carga antes de la desconexión y después de ella
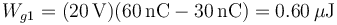
No hace falta incluir la carga del condensador 1, pues ésta no se ve modificada.
Vemos que el trabajo realizado por el generador es mayor que el aumento en la energía almacenada. La diferencia se va en energía disipada en la resistencia.