Dos conductores esféricos concéntricos
De Laplace
(Diferencias entre revisiones)
| Línea 29: | Línea 29: | ||
Cada una de estas cargas se distribuye uniformemente por una superficie esférica. El campo eléctrico producido por cada una es de la forma | Cada una de estas cargas se distribuye uniformemente por una superficie esférica. El campo eléctrico producido por cada una es de la forma | ||
| - | <center><math>\vec{E}_i=\begin{cases} \vec{0} & r < R_i \\ & \\ \ | + | <center><math>\vec{E}_i=\begin{cases} \vec{0} & r < R_i \\ & \\ \dfrac{Q_i}{4\pi\varepsilon_0 r^2}\vec{u}_r & r > R_i\end{cases}</math></center> |
El campo total será la superposición de los de las tres superficies | El campo total será la superposición de los de las tres superficies | ||
| Línea 37: | Línea 37: | ||
Esto da como resultado las siguientes cuatro regiones | Esto da como resultado las siguientes cuatro regiones | ||
| - | <center><math>\vec{E}=\begin{cases} \vec{0} & r < a \\ & \\ \dfrac{Q_1}{4\pi\varepsilon_0 r^2} & a < r < b \\ & \\ \vec{0} & b < r < c \\ & \\ \dfrac{Q_1+Q_2}{4\pi\varepsilon_0 r^2} & r | + | <center><math>\vec{E}=\begin{cases} \vec{0} & r < a \\ & \\ \dfrac{Q_1}{4\pi\varepsilon_0 r^2} & a < r < b \\ & \\ \vec{0} & b < r < c \\ & \\ \dfrac{Q_1+Q_2}{4\pi\varepsilon_0 r^2} & r > c \end{cases}</math></center> |
En los volúmenes conductores (<math>r < a</math> y <math>b < r < c</math>) el campo se anula. | En los volúmenes conductores (<math>r < a</math> y <math>b < r < c</math>) el campo se anula. | ||
Revisión de 09:40 22 jun 2015
Contenido |
1 Enunciado
Se tiene dos conductores esféricos concéntricos. El primero (“1”) es una esfera maciza de radio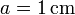 
y el otro (“2”) es una corona esférica de radio interior 
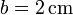y exterior 
.
Inicialmente los dos conductores están aislados y cada uno almacena una carga de 8 nC.
- Calcule el campo eléctrico
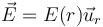en todos los puntos del espacio. Indique cualitativamente cómo sería la gráfica de E(r) como función de la coordenada radial r
- Halle el potencial eléctrico al que se encuentra cada conductor.
- Suponga que, en un instante dado, se cierra el interruptor que conecta el conductor exterior a una fuente de tensión
. Una vez que se ha alcanzado de nuevo el equilibrio, ¿cuál es el nuevo voltaje de la esfera y la carga de la corona?
- ¿Cuánto vale la energía almacenada en el sistema antes y después de cerrar el interruptor?
- ¿Qué trabajo realiza la fuente de tensión en este proceso? ¿Cuánta energía se disipa en lugar de almacenarse como energía electrostática?
2 Campo eléctrico
Por tratarse de conductores en equilibrio electrostático, las cargas se acumulan en las superficies conductoras. Tenemos tres superficies con las siguientes cargas:
- En r = a = 1 cm
- La carga de la superficie de la esfera es la total del conductor 1
- En r = b = 2 cm
- Por el teorema de Faraday, sobre la pared del hueco se almacena una carga opuesta a la que haya en el interior
- En r = c = 4 cm
- La carga total del conductor 2 es la suma de las de sus superficies
Cada una de estas cargas se distribuye uniformemente por una superficie esférica. El campo eléctrico producido por cada una es de la forma
El campo total será la superposición de los de las tres superficies
Esto da como resultado las siguientes cuatro regiones
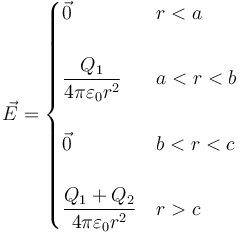
En los volúmenes conductores (r < a y b < r < c) el campo se anula.
