Dos conductores esféricos concéntricos
De Laplace
(Diferencias entre revisiones)
Antonio (Discusión | contribuciones)
(Página creada con '==Enunciado== Se tiene dos conductores esféricos concéntricos. El primero (“1”) es una esfera maciza de radio <math>a=1\,\mathrm{cm}</math> y el otro (“2&rdq…')
Edición más nueva →
(Página creada con '==Enunciado== Se tiene dos conductores esféricos concéntricos. El primero (“1”) es una esfera maciza de radio <math>a=1\,\mathrm{cm}</math> y el otro (“2&rdq…')
Edición más nueva →
Revisión de 14:08 19 jun 2015
Contenido |
1 Enunciado
Se tiene dos conductores esféricos concéntricos. El primero (“1”) es una esfera maciza de radio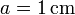 
y el otro (“2”) es una corona esférica de radio interior 
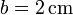y exterior 
.
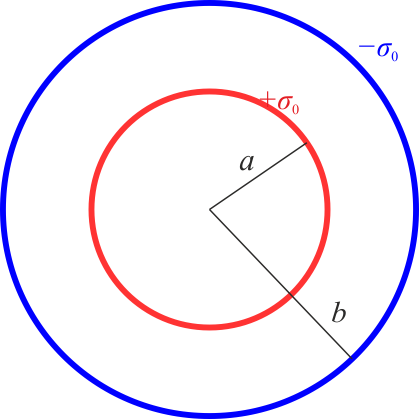
Inicialmente los dos conductores están aislados y cada uno almacena una carga de 8 nC.
- Calcule el campo eléctrico
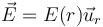en todos los puntos del espacio. Indique cualitativamente cómo sería la gráfica de E(r) como función de la coordenada radial r
- Halle el potencial eléctrico al que se encuentra cada conductor.
- Suponga que, en un instante dado, se cierra el interruptor que conecta el conductor exterior a una fuente de tensión
. Una vez que se ha alcanzado de nuevo el equilibrio, ¿cuál es el nuevo voltaje de la esfera y la carga de la corona?
- ¿Cuánto vale la energía almacenada en el sistema antes y después de cerrar el interruptor?
- ¿Qué trabajo realiza la fuente de tensión en este proceso? ¿Cuánta energía se disipa en lugar de almacenarse como energía electrostática?
