Espira triangular que penetra en campo magnético

De Laplace

(Diferencias entre revisiones)

Antonio (Discusión | contribuciones)
(Página creada con '==Enunciado== Una espira en forma de triángulo de altura <math>h</math> y base <math>b=b_1+b_2</math> penetra en un campo magnético uniforme <math>B_0\vec{k}</math> que se ext…')
Edición más nueva →

Revisión de 22:51 18 jun 2015

1 Enunciado

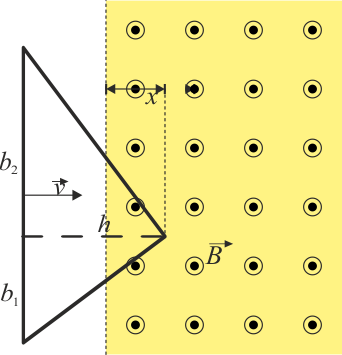
Una espira en forma de triángulo de altura $h$ y base $b = b 1 + b 2$ penetra en un campo magnético uniforme 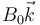$B_0\vec{k}$ que se extiende en la región $x > 0$ tal como indica la figura (la base del triángulo es paralela al borde del campo). La espira es de un hilo de resistencia $R$ .

La espira se mueve con velocidad constante 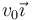$v_0\vec{\imath}$ y penetra en el campo magnético en $t = 0$ .

Determine la corriente que circula por la espira como función del tiempo.
Calcule la energía total disipada en ella desde que comienza a entrar hasta que penetra por completo.
Halle la fuerza magnética sobre la espira para el instante en que ha penetrado hasta $x = h / 2$ .
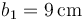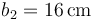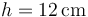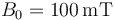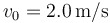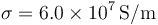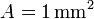Dé valores numéricos a los apartados anteriores si $b_1=9\,\mathrm{cm}$ , $b_2=16\,\mathrm{cm}$ , $h=12\,\mathrm{cm}$ , $B_0=100\,\mathrm{mT}$ , $v_0=2.0\,\mathrm{m}/\mathrm{s}$ y el hilo tiene conductividad $\sigma = 6.0\times 10^7\,\mathrm{S}/\mathrm{m}$ y sección $A=1\,\mathrm{mm}^2$ .