Proceso irreversible de 4 pasos
De Laplace
| Línea 35: | Línea 35: | ||
<center><math>\Delta U = nc_v\,\Delta T = \frac{p_BV_B-p_AV_A}{\gamma-1}</math></center> | <center><math>\Delta U = nc_v\,\Delta T = \frac{p_BV_B-p_AV_A}{\gamma-1}</math></center> | ||
| - | Igualando estas dos cantidades y despejando obtenemos el volumen en el estado B | + | Igualando estas dos cantidades y despejando obtenemos el volumen en el estado B |
<center><math>V_B = V_A\left(1-\frac{p_B-p_A}{\gamma p_B}\right)</math></center> | <center><math>V_B = V_A\left(1-\frac{p_B-p_A}{\gamma p_B}\right)</math></center> | ||
última version al 17:59 1 abr 2015
Contenido |
1 Enunciado
Una cierta cantidad de aire seco (considerado como gas ideal diatómico) se encuentra contenido en un cilindro de sección cuadrada de 10 cm de lado, cerrado por un pistón móvil situado inicialmente a 16 cm del fondo. El aire interior se encuentra inicialmente (estado A) a 300 K de temperatura (que es la del ambiente en todo momento) y a la presión atmosférica de 0.1 MPa.
Se le aplica a este gas el siguiente proceso cíclico
- A→B Se aumenta bruscamente la presión aplicada a 0.8 MPa, de forma que se produce una compresión muy rápida, que puede aproximarse por un proceso adiabático irreversible.
- B→C Manteniendo la presión exterior de 0.8 MPa se espera hasta que vuelva a alcanzar el equilibrio térmico con el ambiente.
- C→D Se retira bruscamente la presión exterior, dejándola en su valor inicial de 0.1 MPa. Se produce una expansión brusca que puede aproximarse por un proceso adiabático irreversible.
- D→A Manteniendo la presión exterior de 0.1 MPa se espera hasta que vuelva a alcanzar el equilibrio térmico con el ambiente.
Para este ciclo
- Calcule los valores de la presión, volumen y temperatura al final de cada paso. Indique los estados, así como los procesos oportunos en un diagrama pV
- Halle el trabajo y el calor que entran en el sistema en cada paso, así como las variaciones de energía interna y entalpía en cada uno.
- Calcule, para un ciclo completo, el trabajo que entra y el que sale del sistema, así como el calor que entra y el que sale.
- ¿Es este sistema un refrigerador? ¿Una máquina térmica? ¿Una estufa?
2 Presiones, volúmenes y temperaturas
2.1 Estado A (inicial)
Inicialmente tenemos el estado definido por
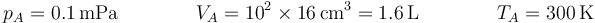
2.2 Estado B
En el primer paso, la presión exterior aumenta bruscamente y a partir de ahí se mantiene constante. Tal como se describe en el apartado teórico correspondiente y en un problema similar, al ser un proceso adiabático se cumple
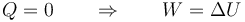
Por ser una compresión a presión constante, el trabajo es igual a
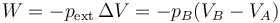
y el aumento de la energía interna
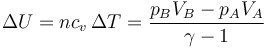
Igualando estas dos cantidades y despejando obtenemos el volumen en el estado B
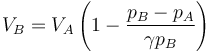
siendo su valor numérico
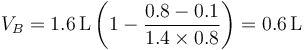
Una vez que tenemos la presión y el volumen hallamos la temperatura en este estado
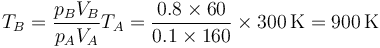
2.3 Estado C
El segundo paso es un enfriamiento a presión constante hasta que la temperatura vuelve a ser la inicial

Hallamos el nuevo volumen por la ley de los gases ideales, que entre los estados A y C se reduce a la ley de Boyle
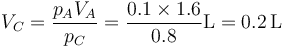
También podíamos haber relacionado los estados B y C, y en ese caso habríamos usado la ley de Charles.
2.4 Estado D
Tenemos un nuevo proceso adiabático irreversible en el que la presión permanece constante, por lo que podemos aplicar una fórmula análoga a la del primer paso
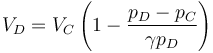
con
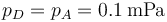
y resulta
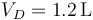
siendo la nueva temperatura
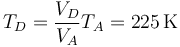
2.5 Tabla resumen
| Estado | p (MPa) | V (L) | T (K) |
|---|---|---|---|
| A | 0.1 | 1.6 | 300 |
| B | 0.8 | 0.6 | 900 |
| C | 0.8 | 0.2 | 300 |
| D | 0.1 | 1.2 | 225 |
A la hora de representar los estados en una gráfica, podemos marcar los cuatro vértices, pero solo se pueden unir por una línea en los procesos cuasiestáticos.
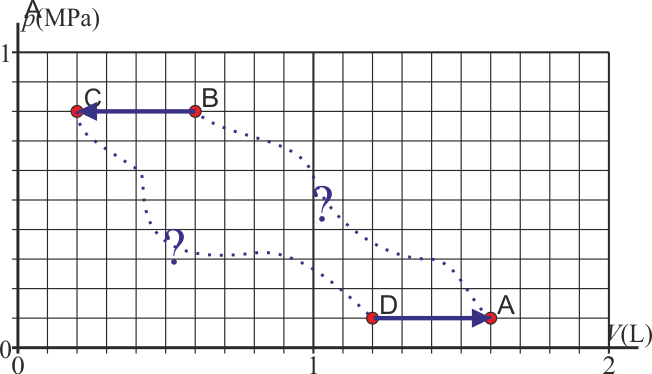
3 Cambios energéticos
La mayoría de los cálculos ya han sido indicados en el apartado anterior.
3.1 Proceso A→B
En el primer paso, es nulo el calor, por ser el proceso adiabático
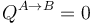
y el trabajo y la variación de la energía interna son iguales
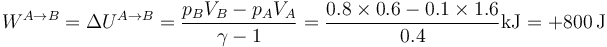
La variación de entalpía se calcula de forma parecida
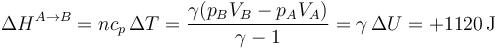
3.2 Proceso B→C
En el segundo paso se vuelve a la temperatura inicial, por lo que la variación de energía interna es la opuesta a la del paso anterior
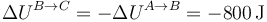
Lo mismo ocurre con la entalpía
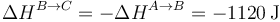
Puesto que se trata de un proceso a presión constante, el calor es igual al incremento de entalpía.
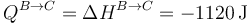
y el trabajo lo calculamos por el primer principio de la termodinámica
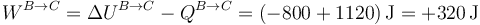
Obsérvese como a partir de los incrementos en dos funciones de estado (U y H) hemos hallado el calor y el trabajo, que no son funciones de estado.
3.3 Proceso C→D
Este es análogo al primero.
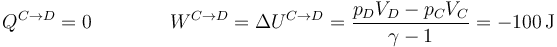
y para la entalpía
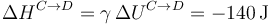
3.4 Proceso D→A
Este es análogo al segundo
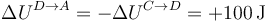
Para la entalpía
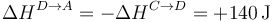
Puesto que se de nuevo trata de un proceso a presión constante
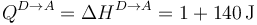
y el trabajo vale
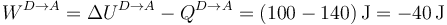
3.5 Tabla resumen
| Paso | Q (J) | W (J) | ΔU (J) | ΔH (J) |
|---|---|---|---|---|
| A→B | 0 | +800 | +800 | +1120 |
| B→C | −1120 | +320 | −800 | −1120 |
| C→D | 0 | −100 | −100 | −140 |
| D→A | +140 | −40 | +100 | +140 |
4 Entrada y salida de calor y trabajo
Separando los casos en que entre calor (signo positivo) o sale (signo negativo)

y lo mismo para el trabajo

5 Interpretación
Vemos que en este sistema hay una transformación neta de 980J de trabajo en calor, pero sin que haya dos focos térmicos, por lo que el sistema es simplemente una estufa.





