Dos esferas huecas
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== \end{center} Se tiene un sistema de cargas formado por dos superficies esféricas de radio $b=4\,cm$ cuyos centros distan $a=3\,\mathrm{cm}$, como indica la figura…') |
|||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
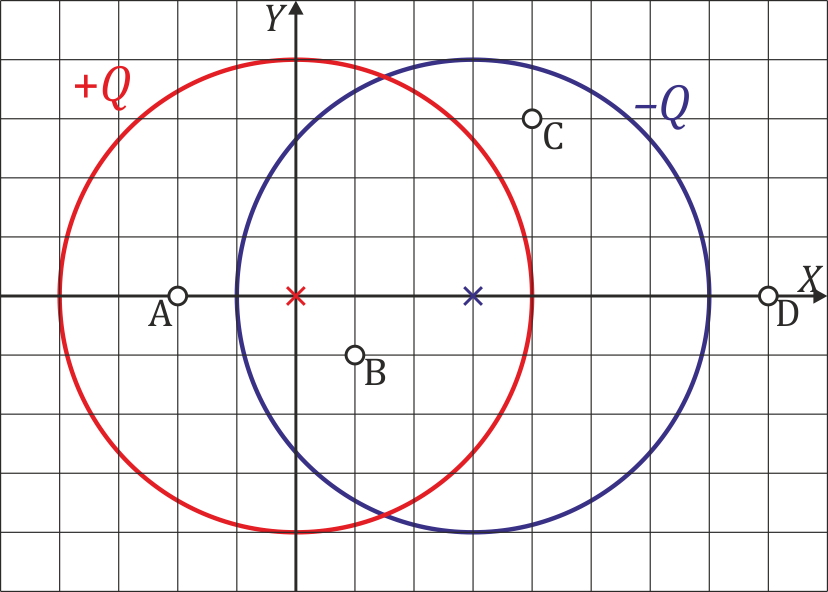
| - | + | Se tiene un sistema de cargas formado por dos superficies esféricas de radio <math>b=4\,\mathrm{cm}</math> cuyos centros distan <math>a=3\,\mathrm{cm}</math>, como indica la figura. Las superficies está cargadas uniformemente con cargas respectivas de <math>+1\,\mathrm{nC}</math> y <math>-1\,\mathrm{nC}</math> | |
| - | Se tiene un sistema de cargas formado por dos superficies esféricas | + | |
| - | de radio | + | [[Archivo:dos-esferas-descentradas.png]] |
| - | indica la figura. Las superficies está cargadas uniformemente con | + | |
| - | cargas respectivas de | + | |
| - | |||
| - | |||
| - | |||
Para los puntos marcados en la figura (en cm) | Para los puntos marcados en la figura (en cm) | ||
| - | + | ||
| - | \vec{r}_A=-2\vec{\imath} \qquad | + | <math>\vec{r}_A=-2\vec{\imath} \qquad |
\vec{r}_B=\vec{\imath}-\vec{\jmath} \qquad | \vec{r}_B=\vec{\imath}-\vec{\jmath} \qquad | ||
\vec{r}_C=4\vec{\imath}+3\vec{\jmath} \qquad | \vec{r}_C=4\vec{\imath}+3\vec{\jmath} \qquad | ||
\vec{r}_D=8\vec{\imath} | \vec{r}_D=8\vec{\imath} | ||
| - | + | </math> | |
| - | + | # Calcule el campo eléctrico. | |
| - | + | # Calcule el potencial eléctrico. | |
| - | + | # A partir de la integración de la fuerza, halle el trabajo que debe realizar un agente externo para mover cuasiestáticamente una carga de <math>-1\,\mathrm{nC}</math> desde el punto A al punto D moviéndola a lo largo del eje X. | |
| - | + | ||
| - | realizar un agente externo para mover cuasiestáticamente una carga de | + | |
| - | + | ||
| - | + | ||
[[Categoría:Problemas de electrostática en el vacío (GIE)]] | [[Categoría:Problemas de electrostática en el vacío (GIE)]] | ||
Revisión de 23:45 16 jun 2014
Enunciado
Se tiene un sistema de cargas formado por dos superficies esféricas de radio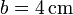 
cuyos centros distan 
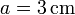, como indica la figura. Las superficies está cargadas uniformemente con cargas respectivas de 
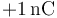y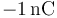 
Para los puntos marcados en la figura (en cm)
- Calcule el campo eléctrico.
- Calcule el potencial eléctrico.
- A partir de la integración de la fuerza, halle el trabajo que debe realizar un agente externo para mover cuasiestáticamente una carga de 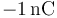desde el punto A al punto D moviéndola a lo largo del eje X.
