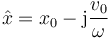Estudio de un movimiento armónico simple
De Laplace
(Diferencias entre revisiones)
| Línea 3: | Línea 3: | ||
==Solución== | ==Solución== | ||
| - | Obtenemos la frecuencia | + | Obtenemos la frecuencia a partir de la ecuación del oscilador armónico |
| + | |||
| + | <center><math>a = -\omega^2x\,</math></center> | ||
| + | |||
| + | Esta ecuación se cumple en todo instante. En particular en el instante inicial, por lo que | ||
| + | |||
| + | <center><math>\omega = \sqrt{-\frac{a_0}{x_0}}=\sqrt{\frac{0.20}{0.80}}\mathrm{s}^{-1}= 0.5\,\mathrm{s}^{-1}</math></center> | ||
| + | |||
| + | Una vez que tenemos la frecuencia, tenemos el periodo | ||
| + | |||
| + | <center><math>T = \frac{2\pi}{\omega} = 4\pi\,\mathrm{s}=12.57\,\mathrm{s}</math></center> | ||
| + | |||
| + | A partir de las condiciones iniciales obtenemos el fasor (amplitud compleja) de la posición | ||
| + | |||
| + | <center><math>\hat{x}=x_0-\mathrm{j}\frac{v_0}{\omega}</math></center> | ||
[[Categoría:Problemas de cinemática del movimiento rectilíneo (GIE)]] | [[Categoría:Problemas de cinemática del movimiento rectilíneo (GIE)]] | ||
Revisión de 17:54 31 oct 2013
1 Enunciado
Un oscilador armónico con posición de equilibrio xeq = 0 se mueve de tal forma que en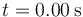 
la partícula se halla en 
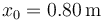, moviéndose con velocidad 
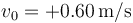y aceleración 
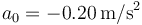. Halle la frecuencia ω y el periodo del movimiento, su amplitud de oscilación y la fase inicial. Exprese los fasores (amplitudes complejas) de la posición, velocidad y aceleración.
2 Solución
Obtenemos la frecuencia a partir de la ecuación del oscilador armónico
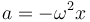
Esta ecuación se cumple en todo instante. En particular en el instante inicial, por lo que
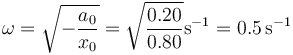
Una vez que tenemos la frecuencia, tenemos el periodo
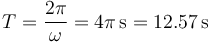
A partir de las condiciones iniciales obtenemos el fasor (amplitud compleja) de la posición
