Estudio de un movimiento armónico simple
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Un oscilador armónico con posición de equilibrio <math>x=0</math> se mueve de tal forma que en <math>t=0.00\,\mathrm{s}</math> la partícula se halla en <math>x_…') |
|||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Un oscilador armónico con posición de equilibrio <math> | + | Un oscilador armónico con posición de equilibrio <math>x_\mathrm{eq}=0</math> se mueve de tal forma que en <math>t=0.00\,\mathrm{s}</math> la partícula se halla en <math>x_0=0.80\,\mathrm{m}</math>, moviéndose con velocidad <math>v_0=+0.60\,\mathrm{m}/\mathrm{s}</math> y aceleración <math>a_0=-0.20\,\mathrm{m}/\mathrm{s}^2</math>. Halle la frecuencia <math>\omega</math> y el periodo del movimiento, su amplitud de oscilación y la fase inicial. Exprese los fasores (amplitudes complejas) de la posición, velocidad y aceleración. |
==Solución== | ==Solución== | ||
| + | Obtenemos la frecuencia | ||
[[Categoría:Problemas de cinemática del movimiento rectilíneo (GIE)]] | [[Categoría:Problemas de cinemática del movimiento rectilíneo (GIE)]] | ||
Revisión de 11:54 31 oct 2013
1 Enunciado
Un oscilador armónico con posición de equilibrio xeq = 0 se mueve de tal forma que en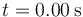 
la partícula se halla en 
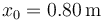, moviéndose con velocidad 
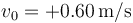y aceleración 
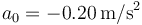. Halle la frecuencia ω y el periodo del movimiento, su amplitud de oscilación y la fase inicial. Exprese los fasores (amplitudes complejas) de la posición, velocidad y aceleración.
2 Solución
Obtenemos la frecuencia
