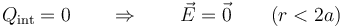Sistema de tres superficies esféricas cargadas
De Laplace
(Diferencias entre revisiones)
(→Tercer caso) |
(→Caso general) |
||
| Línea 15: | Línea 15: | ||
==Caso general== | ==Caso general== | ||
| + | En lugar de resolver tres veces el mismo problema, consideramos un sistema con cargas cualesquiera y posteriormente sustituimos por sus valores concretos. | ||
| + | ===Campo eléctrico=== | ||
| + | El campo debido a las tres esferas, se calcula por aplicación de la ley de Gauss. Por la simetría esférica del sistema, el campo es radial y dependiente solo de la distancia al centro del sistema | ||
| + | |||
| + | <center><math>\vec{E}=E(r)\vec{u}_r</math></center> | ||
| + | |||
| + | Para cada superficie esférica que tomemos | ||
| + | |||
| + | <center><math>\oint \vec{E}\cdot\mathrm{d}\vec{S}=\oint E\,\mathrm{d}S = 4\pi r^2E</math></center> | ||
| + | |||
| + | De acuerdo con la ley de Gauss | ||
| + | |||
| + | <center><math>\oint \vec{E}\cdot\mathrm{d}\vec{S}=\frac{Q_\mathrm{int}}{\varepsilon_0}\qquad\Rightarrow\qquad \vec{E}=\frac{Q_\mathrm{int}}{\varepsilon_0}</math></center> | ||
| + | |||
| + | Tenemos ahora cuatro regiones, de adentro a fuera: | ||
| + | |||
| + | ;r < 2a: En el interior de la esfera pequeña no se envuelve ninguna carga, por lo que el campo es nulo | ||
| + | |||
| + | <center><math>Q_\mathrm{int}=0\qquad\Rightarroçw\qquad \vec{E}=\vec{0}\qquad (r< 2a)</math></center> | ||
| + | |||
==Primer caso== | ==Primer caso== | ||
==Segundo caso== | ==Segundo caso== | ||
==Tercer caso== | ==Tercer caso== | ||
[[Categoría:Problemas de electrostática en el vacío (GIE)]] | [[Categoría:Problemas de electrostática en el vacío (GIE)]] | ||
Revisión de 22:31 30 abr 2013
Contenido |
1 Enunciado
Supongamos un sistema formado por tres superficies esféricas concéntricas, de radios R1 = 2a, R2 = 3a y R3 = 6a, respectivamente, que almacenan cargas Q1, Q2 y Q3 distribuidas uniformemente en cada una.
Calcule
- El campo eléctrico en todos los puntos del espacio.
- El trabajo necesario para llevar una carga q0 desde el infinito hasta el centro del sistema.
- La energía electrostática almacenada en el sistema de tres esferas (sin incluir la carga q0).
para cada uno de los siguientes tres casos:
- Q1 = Q2 = Q0, Q3 = − 2Q0.
- Q1 = Q3 = Q0, Q2 = − 2Q0.
- Q2 = Q3 = Q0, Q1 = − 2Q0.
2 Caso general
En lugar de resolver tres veces el mismo problema, consideramos un sistema con cargas cualesquiera y posteriormente sustituimos por sus valores concretos.
2.1 Campo eléctrico
El campo debido a las tres esferas, se calcula por aplicación de la ley de Gauss. Por la simetría esférica del sistema, el campo es radial y dependiente solo de la distancia al centro del sistema
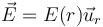
Para cada superficie esférica que tomemos
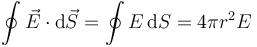
De acuerdo con la ley de Gauss

Tenemos ahora cuatro regiones, de adentro a fuera:
- r < 2a
- En el interior de la esfera pequeña no se envuelve ninguna carga, por lo que el campo es nulo