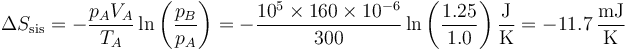Variación de entropía por compresión
De Laplace
| Línea 58: | Línea 58: | ||
mientras que el trabajo se halla a parte de la integral de la presión exterior, que es constante (e igual a la final) | mientras que el trabajo se halla a parte de la integral de la presión exterior, que es constante (e igual a la final) | ||
| - | <center><math>W_\mathrm{in,sis} = -\int_A^B p_\mathrm{ext}\,\mathrm{d}V = -p_B(V_B-V_A)=(-1.25\times 10^5)\times(128-160)\times 10^{-6}\,\mathrm{Pa}\cdot\mathrm{m}^3=+ | + | <center><math>W_\mathrm{in,sis} = -\int_A^B p_\mathrm{ext}\,\mathrm{d}V = -p_B(V_B-V_A)=(-1.25\times 10^5)\times(128-160)\times 10^{-6}\,\mathrm{Pa}\cdot\mathrm{m}^3=+3.92\,\mathrm{J}</math></center> |
| - | Es decir, en el sistema entran 4 julios en forma de trabajo, que no son almacenados, sino que vuelven a salir en forma de calor, entregando entropía al ambiente. | + | (los decimales finales resultan de hacer los cálculos exactos, con g = 9.81N/kg, aunque en su presentación se redondeen los resultados a tres cifras significativas). Es decir, en el sistema entran unos 4 julios en forma de trabajo, que no son almacenados, sino que vuelven a salir en forma de calor, entregando entropía al ambiente. |
Por tanto, la variación de entropía del ambiente es | Por tanto, la variación de entropía del ambiente es | ||
| - | <center><math>\Delta S_\mathrm{amb}=\frac{ | + | <center><math>\Delta S_\mathrm{amb}=\frac{3.92\,\mathrm{J}}{300\,\mathrm{K}}=+13.1\,\frac{\mathrm{mJ}}{\mathrm{K}}</math></center> |
===Variación de entropía del sistema=== | ===Variación de entropía del sistema=== | ||
| Línea 79: | Línea 79: | ||
Puesto que la temperatura final es la misma que la inicial el primer término se cancela y queda | Puesto que la temperatura final es la misma que la inicial el primer término se cancela y queda | ||
| - | <center><math>\Delta S_\mathrm{sis} = -\frac{p_AV_A}{T_A}\ln\left(\frac{p_B}{p_A}\right)=-\frac{10^5\times 160\times 10^{-6}}{300}\ln\left(\frac{1.25}{1.0}\right)\frac{\mathrm{J}}{\mathrm{K}}=-11. | + | <center><math>\Delta S_\mathrm{sis} = -\frac{p_AV_A}{T_A}\ln\left(\frac{p_B}{p_A}\right)=-\frac{10^5\times 160\times 10^{-6}}{300}\ln\left(\frac{1.25}{1.0}\right)\frac{\mathrm{J}}{\mathrm{K}}=-11.7\,\frac{\mathrm{mJ}}{\mathrm{K}}</math></center> |
===Variación total=== | ===Variación total=== | ||
Sumando las dos contribuciones | Sumando las dos contribuciones | ||
| - | <center><math>\Delta S_\mathrm{u}=\Delta S_\mathrm{sis}+\Delta S_\mathrm{amb}=(-11. | + | <center><math>\Delta S_\mathrm{u}=\Delta S_\mathrm{sis}+\Delta S_\mathrm{amb}=(-11.7+13.1)\frac{\mathrm{mJ}}{\mathrm{K}} = +1.37\frac{\mathrm{mJ}}{\mathrm{K}}</math></center> |
La variación de entropía del universo es estrictamente positiva, como corresponde a un proceso irreversible. | La variación de entropía del universo es estrictamente positiva, como corresponde a un proceso irreversible. | ||
| - | |||
==Compresión isoterma reversible== | ==Compresión isoterma reversible== | ||
| + | En el segundo caso, la presión y la temperatura finales son los mismos que en el primer caso | ||
| + | |||
| + | <center><math>p_B=1.25\,\mathrm{bar}\qquad\qquad T_B = T_A = 300\,\mathrm{K}</math></center> | ||
| + | |||
| + | y por ello el volumen final también es el mismo que en el primer caso: | ||
| + | |||
| + | <center><math>p_BV_B = p_AV_A \qquad\Rightarrow\qquad V_B = \frac{p_AV_A}{p_B}= 128\,\mathrm{cm}^3</math></center> | ||
| + | |||
| + | ===Cambio de entropía del sistema=== | ||
| + | Puesto que el estado inicial es el mismo que en todos los casos y el estado final coincide con el el apartado anterior, la variación de entropía del sistema 8que depende sólo de los estados) es la misma que allí | ||
| + | |||
| + | <center><math>\Delta S_\mathrm{sis} = -\frac{p_AV_A}{T_A}\ln\left(\frac{p_B}{p_A}\right)=-\frac{10^5\times 160\times 10^{-6}}{300}\ln\left(\frac{1.25}{1.0}\right)\frac{\mathrm{J}}{\mathrm{K}}=-11.7\,\frac{\mathrm{mJ}}{\mathrm{K}}</math></center> | ||
==Compresión adiabática irreversible== | ==Compresión adiabática irreversible== | ||
==Compresión adiabática reversible== | ==Compresión adiabática reversible== | ||
==Comparación== | ==Comparación== | ||
[[Categoría:Problemas del segundo principio de la termodinámica (GIE)]] | [[Categoría:Problemas del segundo principio de la termodinámica (GIE)]] | ||
Revisión de 18:28 20 mar 2013
Contenido |
1 Enunciado
Considere un prisma vertical de 4 cm de lado que contiene aire. El cilindro contiene un pistón que inicialmente está a 10 cm de altura. La temperatura del gas inicialmente es de 300 K, que también es la temperatura ambiente y la presión exterior es de 100 kPa.
Calcule la variación en la entropía del gas, del entorno y del universo en los cuatro siguientes procesos:
- Se coloca bruscamente una pesa de 4 kg encima del émbolo y las paredes son diatermas.
- Se colocan progresivamente 4 kg de arena, grano a grano y las paredes son diatermas.
- Se coloca bruscamente una pesa de 4 kg encima del émbolo y las paredes son adiabáticas.
- Se colocan progresivamente 4 kg de arena, grano a grano y las paredes son adiabáticas.
2 Introducción
En este problema tenemos cuatro variantes del mismo sistema, que son muy similares en apariencia, pero difieren en detalles cruciales que provocan que los resultados sean distintos en cada uno de los casos.
Los cálculos analíticos (pero no los valores numéricos) del trabajo y calor en estos cuatro procesos se consideran además en los problemas “Trabajo en una compresión isoterma por un peso” y “Compresión adiabática de un gas por un peso”.
En todos los casos tenemos inicialmente un gas en un estado A en el que ocupa un cierto volumen a una cierta presión y temperatura iguales a las del ambiente
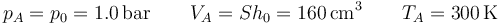
Asimismo, en las cuatro situaciones se añade una pesa que incrementa la presión sobre el gas a un valor
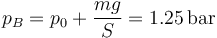
(aproximando g por 10 m/s²). La temperatura y volumen final, en cambio, dependen del proceso que consideremos.
3 Compresión isoterma irreversible
En el primer caso, el recipiente no está aislado del exterior, por lo que una vez se deja caer la pesa y se alcanza de nuevo el equilibrio, su temperatura final es igual a la inicial
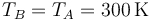
Puesto que tenemos la presión y la temperatura tenemos automáticamente el volumen, por la ley de los gases ideales (o, en este caso particular, la ley de Boyle)
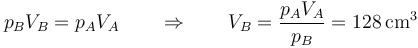
En términos de la nueva altura del pistón
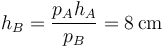
Para calcular la variación de entropía tenemos que hallar por separado la del sistema y la del ambiente.
3.1 Variación de entropía del ambiente
El ambiente es un foco térmico a temperatura constante T0. Su variación de entropía es la correspondiente a un proceso isotermo reversible
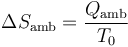
El calor que entra en el ambiente es el mismo que sale del sistema
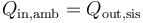
A su vez el calor que sale del sistema lo da el primer principio de la termodinámica
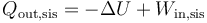
Por ser un proceso isotermo de un gas ideal, su variación de energía interna es nula
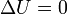
mientras que el trabajo se halla a parte de la integral de la presión exterior, que es constante (e igual a la final)
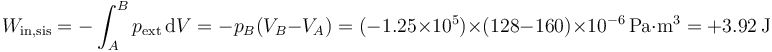
(los decimales finales resultan de hacer los cálculos exactos, con g = 9.81N/kg, aunque en su presentación se redondeen los resultados a tres cifras significativas). Es decir, en el sistema entran unos 4 julios en forma de trabajo, que no son almacenados, sino que vuelven a salir en forma de calor, entregando entropía al ambiente.
Por tanto, la variación de entropía del ambiente es
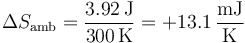
3.2 Variación de entropía del sistema
La fórmula anterior no nos vale para el cálculo de la variación de entropía del propio gas. No sabemos si la temperatura del sistema ha permanecido constante. Lo único que sabemos es que su temperatura inicial y final es la misma, pero en medio puede haber cambiado, incluso de forma no uniforme (calentándose algunos puntos más que otros).
Para hallar la variación de entropía del sistema podemos:
- imaginar un proceso reversible que lleve del estado inicial al mismo estado final.
- aplicar que la entropía es una función de estado y por tanto solo necesitamos conocer su valor final y su valor inicial.
El segundo método solo es aplicable cuando conocemos la entropía como función de las variables de estado. Para el caso de un gas ideal esto es posible. En función de la temperatura y la presión, la variación de entropía es
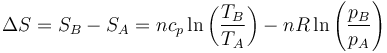
Puesto que la temperatura final es la misma que la inicial el primer término se cancela y queda
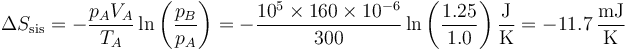
3.3 Variación total
Sumando las dos contribuciones
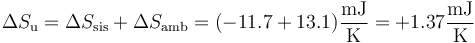
La variación de entropía del universo es estrictamente positiva, como corresponde a un proceso irreversible.
4 Compresión isoterma reversible
En el segundo caso, la presión y la temperatura finales son los mismos que en el primer caso

y por ello el volumen final también es el mismo que en el primer caso:
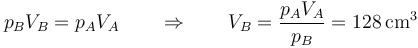
4.1 Cambio de entropía del sistema
Puesto que el estado inicial es el mismo que en todos los casos y el estado final coincide con el el apartado anterior, la variación de entropía del sistema 8que depende sólo de los estados) es la misma que allí